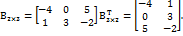Интеграл типа
типа ∫ R (x; ствительные числа, причем a ≠ 0, R(u; v) – рациональная функция переменных u, v. Подстановка
= Матрицы.Основные понятия и действия над матрицами. Матрицей размера m×nназывается прямоугольная таблицачисел (или других математических объектов) – элементов матрицы, расположенных в m строках и n столбцах:
aij– элемент, принадлежащий i-й строке и j-му столбцу матрицы; числа i, j называются индексами элемента. Матрицы обозначаются заглавными латинскими буквами: A, B, Cи т. д. или A= Матрица, у которой все элементы равны нулю, называется нулевой. Она обозначается Omxn. Квадратной матрицей n-го порядка называется матрица раз-мераn×n. В квадратной матрице элементы a11, a22,…,anmобразуют главную диагональ. Квадратная матрица называется диагональной, если все ееэлементы, не принадлежащие главной диагонали, равны нулю. Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной матрицей. Обозначается n I или n E. Например,
Если исходная матрица имеет размер m×n, то транспонированная к ней будет иметь размер n×m. Например,
|

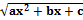 ) dx,где a, b, c– дей-
) dx,где a, b, c– дей- позволяет выделить полный квадрат под знаком корня. В результате исходный интеграл преобразуется к одному из следующих трех типов, которые с помощью дальнейших подстановок сводятся к интегралам от функций, рационально зависящих от тригонометрических функций:
позволяет выделить полный квадрат под знаком корня. В результате исходный интеграл преобразуется к одному из следующих трех типов, которые с помощью дальнейших подстановок сводятся к интегралам от функций, рационально зависящих от тригонометрических функций:
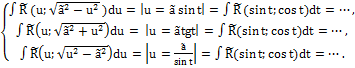

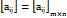 , если указываются элементыи размер матрицы. Матрицы A и B одинаковых размеров называются равными, если равны их соответствующие элементы:A= B⇔aij= bij=i=1,m, j=1,n.
, если указываются элементыи размер матрицы. Матрицы A и B одинаковых размеров называются равными, если равны их соответствующие элементы:A= B⇔aij= bij=i=1,m, j=1,n. – единичная матрица 3-го порядка. Матрица, полученная из данной заменой каждой ее строкистолбцом с тем же номером, называется матрицей, транспонированной к данной. Матрицу, транспонированную к матрице A=
– единичная матрица 3-го порядка. Матрица, полученная из данной заменой каждой ее строкистолбцом с тем же номером, называется матрицей, транспонированной к данной. Матрицу, транспонированную к матрице A= 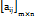 ,обозначают
,обозначают 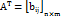 где bij= aji; i= 1,..., m; j= 1,..., n.
где bij= aji; i= 1,..., m; j= 1,..., n.