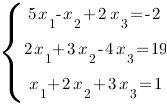Решение:Составим и вычислим сначала главный определитель этой системы: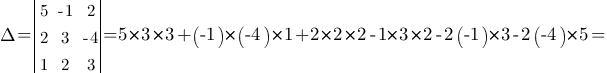 
Так как 
, то система имеет единственное решение, которое можно найти по правилу Крамера: 
где 
получаются из определителя 
путем замены 1-го, 2-го или 3-го столбца, соответственно, на столбец свободных членов.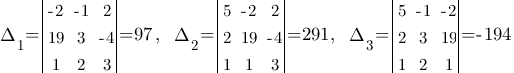 
Таким образом: 
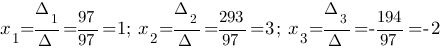Итак,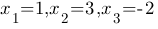 
- единственное решение.
Матричныйметод Запишем систему (1) в ви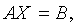де 
где 
Решение: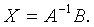 
Построим обратную матрицу 
. Вычислим алгебраические дополнения ко всем элементам, причём алгебраические дополнения, вычисленные для элементов первой строки, записываются первым столбцом матрицы.Знак 
определяется как 
: 
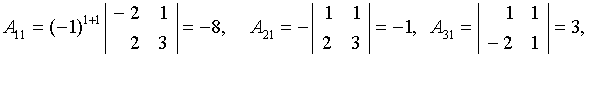
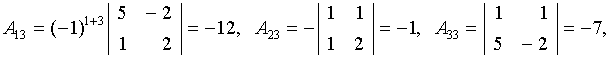т.е. 
имеет вид: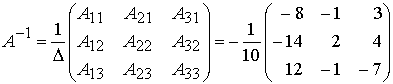 
.Примечания: 1. При умножении матрицы на число все элементы матрицы умножаются на это число2. Умножение матриц возможно, если число столбцов первого сомножителя равно числу строк второго сомножителя.3. При умножении матриц элемент матрицы произведения равен сумме произведений элементов строки 1-го сомножителя матрицы на соответствующие элементы столбца 2-го сомножителя матрицы.Находим матрицу-решение: 
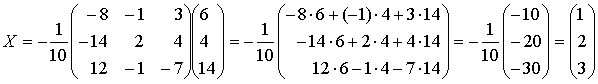.Таким образом, 
.
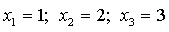