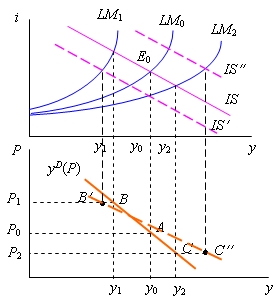
Функция совокупного спроса
Построение. На основе анализа взаимодействия рынка благ с рынком денег можно проследить, как изменение уровня цен влияет на величину совокупного спроса на блага, и построить его функцию, характеризующую зависимость объема эффективного спроса от уровня цен: yD(P). Проведем сначала графический анализ этой зависимости. На рис. 6.8 исходное совместное равновесие на рынках благ, денег и капитала представлено точкой E0. Равновесный объем совокупного спроса на рынке благ установился при некотором исходном уровне цен P0. Отметим его на оси ординат нижней части рис. 6.8. Образующаяся на пересечении значений y0 и P0 точка A есть одна из точек графика yD(P). Пусть уровень цен поднимается до P1. Тогда при заданном номинальном количестве денег их реальная величина уменьшится, вследствие чего кривая LM сдвинется влево: LM0 LM1. Совместное равновесие на рынках благ и финансовом станет возможным только при значениях y1, i1. Следовательно, при уровне цен P1 эффективный спрос будет равен y1. Поэтому точка B тоже лежит на графике yD(P). Если уровень цен снизится до P2, реальное количество денег в обращении возрастет и последует сдвиг LM0 LM2. Величина эффективного спроса увеличится до y2. Координаты P2, y2 в нижней части рис. 6.8 соответствуют точке C. Соединив все найденные таким образом точки функции совокупного спроса, получим ее график yD(P).
|