Средняя линия
1) Средняя линия треугольника Средняя линия треугольника – линия, соединяющая середины его сторон. Теорема. Средняя линия треугольника параллельна его основанию и равна ½ от него. Д-во:
Пусть дан ∆ ABC, середина АВ = К, середина ВС = М. Проведем через С l1 || AB. Найдем на l1 точку D: СД=АВ. ∆ ABC = ∆ BCD (CYC) (AB = CD, *ВСД=*АВС (накрест лежащие), ВС – общая) => ВД = АС => АВСД - #. Пусть середина СД – Q. ∆ KBM = ∆ QCM (CYC) (*KBM=*MCQ, BM = CM (cp. лин), *KMB = *СМQ (вертик)) => CQ = KB = AK => AK = CQ; KM = QM AKQC - # (AK || CQ, AK = CQ) = KM || AC; KQ = AC => 2KM=AC => KM = ½ AC. Ч.т.д.
2) Средняя линия трапеции · Трапеция – четырехугольник, у которого две стороны параллельны, а другие две непараллельные. · Основание – большая из параллельных сторон · Средняя линия трапеции – отрезок, соединяющий середины ее непараллельных сторон. Теорема Средняя линия трапеции параллельна ее основанию и равна ½ от суммы ее параллельных сторон. Д-во:
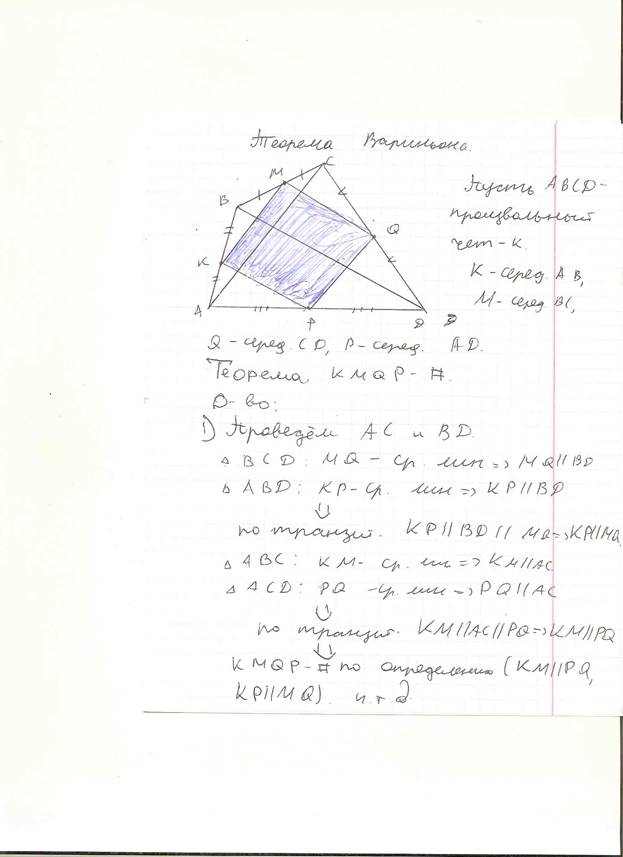
3) Теорема Вариньона
|