Основные задачи и виды группировок
Тема 3. СТАТИСТИЧЕСКАЯ СВОДКА И ГРУППИРОВКА Задачи сводки и ее содержание Научно организованная обработка материалов статистического наблюдения по заранее разработанной программе включает в себя, кроме контроля данных, систематизацию, группировку данных, составление таблиц, получение итогов и производных показателей (средних и относительных величин) и т. д. Собранный в процессе статистического наблюдения материал представляет собой разрозненные первичные сведения об отдельных единицах изучаемого явления. В таком виде материал еще не характеризует явление в целом: не дает представления ни о величине (численности) явления, ни о его составе, ни о размере характерных признаков, ни о существе связей этого явления с другими явлениями и т. д. Возникает необходимость в специальной обработке статистических данных – сводке материалов наблюдения. Сводка материалов наблюдения представляет собой комплекс последовательных действий по обобщению конкретных единичных данных, образующих совокупность, с целью обнаружения типичных черт и закономерностей, присущих изучаемому явлению в целом. Статистическая сводка (простая сводка) в узком смысле слова представляет собой операцию по подсчету общих итоговых (суммарных) данных по совокупности единиц наблюдения. Статистическая сводка (сложная сводка) в широком смысле слова включает в себя также группировку данных наблюдения, подсчет общих и групповых итогов, получение системы взаимосвязанных показателей, представление результатов группировки и сводки в виде статистических таблиц. Правильная, научно организованная сводка, опираясь на предварительный глубокий теоретический анализ, позволяет получить все статистические итоги, отражающие важнейшие, характерные черты объекта исследования, измерить влияние различных факторов на результат и учесть все это в практической работе при составлении текущих и перспективных планов. Задача сводки – дать характеристику объекту исследования с помощью систем статистических показателей, выявить и измерить таким путем его существенные черты и особенности. Эта задача решается на трех этапах: • определение групп и подгрупп; • определение системы показателей; • определение видов таблиц. На первом этапе осуществляется систематизация, группировка материалов, собранных при наблюдении. На втором этапе уточняется предусмотренная планом система показателей, с помощью которых количественно характеризуются свойства и особенности изучаемого предмета. На третьем этапе исчисляются сами показатели, и обобщенные данные для наглядности и удобства представляются в таблицах, статистических рядах, графиках, диаграммах. Перечисленные этапы сводки еще до начала ее проведения отражаются в специально составляемой программе. Программа статистической сводки содержит перечень групп, на которые целесообразно разделить совокупность, их границы в соответствии с группировочными признаками; систему показателей, характеризующих совокупность, и методику их расчета; систему макетов разработочных таблиц, в которых будут представлены итоги расчетов. Наряду с программой существует план проведения сводки, который предусматривает ее организацию. План проведения сводки должен содержать указания о последовательности и сроках выполнения ее отдельных частей, об ответственных за ее выполнение, порядке изложения результатов, а также предусматривать координацию работы всех организаций, задействованных в ее проведении.
Основные задачи и виды группировок Предмет статистических исследований – массовые явления и процессы общественной жизни – обладают многочисленными признаками и свойствами. Обобщить статистические данные, раскрыть наиболее существенные особенности, формы развития массового явления в целом и отдельных его составляющих невозможно без определенных научных принципов обработки данных. Без преодоления индивидуального многообразия объектов статистического наблюдения общие закономерности развития явления или процесса в целом теряются в деталях и мелочах, отличающих каждый объект один от другого, а предельное обобщение влечет за собой извращенное представление о действительности. Для разделения совокупности единиц на однотипные группы статистика использует метод группировок. Статистические группировки – первый этап статистической сводки, позволяющий выделить из массы исходного статистического материала однородные группы единиц, обладающих общим сходством в качественном и количественном отношениях. Важно понимать, что группировка – это не субъективный технический прием разделения совокупности на части, а научно обоснованный процесс разделения множества единиц совокупности по определенному признаку. Основополагающим принципом применения метода группировок является всесторонний, глубокий анализ сущности и природы изучаемого явления, позволяющий определить его типические свойства и внутренние различия. Любая общая совокупность является комплексом частных совокупностей, каждая из которых объединяет явления особого типа, однокачественные в определенном отношении. Каждый тип (группа) имеет специфическую систему признаков с соответствующим уровнем их количественных значений. Установить, к какому типу, в какую частную совокупность нужно отнести группируемые единицы общей совокупности, возможно на основе правильного, четкого определения существенных признаков, по которым должна проводиться группировка. Это второе важное требование научно обоснованной группировки. Третье требование группировки основано на объективном, обоснованном установлении границ групп при условии, что образованные группы должны объединять однородные элементы совокупности, а сами группы (одна по отношению к другой) должны существенно различаться. В противном случае группировка теряет смысл. Таким образом, на основе применения метода группировок определяются группы по принципу подобия и различия единиц совокупности. Подобие – это однородность единиц в определенных пределах (группах); различие – это их существенное расхождение по группам. Итак, группировка – разделение общей совокупности единиц по одному или нескольким существенным признакам на однородные группы, различающиеся между собой в качественном и количественном отношении и позволяющие выделить социально-экономические типы, изучить структуру совокупности или проанализировать связи между отдельными признаками. Разнообразие общественных явлений и целей их изучения делает возможным применение большого количества статистических группировок явлений и решение на этой основе самых различных конкретных задач. Основными задачами, решаемыми с помощью группировок, в статистике являются следующие: • выделение в совокупности изучаемых явлений их социально-экономических типов; • изучение структуры общественных явлений; • выявление связей и зависимостей между общественными явлениями. Все группировки, связанные с выделением в совокупности изучаемых явлений их социально-экономических типов, занимают в статистике центральное место. Эта задача имеет отношение к наиболее существенным, решающим сторонам общественной жизни, например группировка населения по социальному статусу, полу, возрасту, уровню образования, группировка предприятий и организаций по формам собственности, отраслевой принадлежности. Построение подобных группировок за продолжительные периоды позволяет проследить процесс развития социально-экономических отношений. Задача расчленения совокупности общественных явлений по их социально-экономическим типам решается с помощью построения типологических группировок. Таким образом, типологическая группировка – это разделение качественно разнородной исследуемой совокупности на однородные группы единиц в соответствии с социально-экономическими типами. Примером типологической группировки является группировка по виду участвующих субъектов инновационной деятельности в одном из регионов, которые можно разделить на следующие основные группы взаимоотношений (табл. 3.1). Таблица 3.1 Группировка субъектов инновационной деятельности
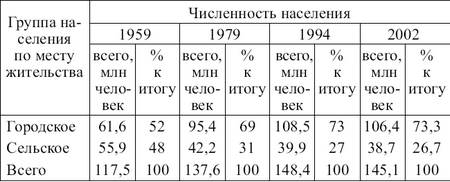
Исключительно важное значение придается изучению структуры общественных явлений, т. е. изучению различий в составе какого-либо определенного типа явлений (соотношения между составными частями явления, изменения в этих соотношениях за определенный период времени). Таким образом, структурной группировкой называется группировка, в которой происходит разделение однородной совокупности на группы, характеризующие ее структуру по какому-либо варьирующему признаку. К структурным группировкам относятся группировка населения по полу, возрасту, уровню образования, группировка предприятий по численности работников, уровню заработной платы, объему работ и т. д. В изменении структуры общественных явлений отражаются важнейшие закономерности их развития. Например, группировка в табл. 3.2 показывает, что в период с 1959 по 1994 г. численность городского населения постоянно увеличивалась, а численность сельского падала, однако в период с 1994 по 2002 г. соотношение этих групп населения не изменилось. Таблица 3.2 Группировка населения России по месту проживания за 1959–2002 гг.
Применение структурных группировок позволяет не только раскрыть структуру совокупности, но и проанализировать изучаемые процессы, их интенсивность, изменение в пространстве, а взятые за ряд периодов времени структурные группировки раскрывают закономерности изменений состава совокупности во времени. В основу структурных группировок могут быть положены атрибутивный или количественный признаки. Их выбор определяется задачами конкретного исследования и сущностью изучаемой совокупности. Группировка, приведенная в табл. 3.2, построена по атрибутивному признаку. При структурной группировке по количественному признаку возникает необходимость определения числа групп и их границ. Этот вопрос решается в соответствии с задачами исследования. Один и тот же статистический материал может быть разбит на группы различным образом в зависимости от целей и задач исследования. Главное, чтобы в процессе группировки были ярко отражены особенности изучаемого явления и созданы предпосылки для конкретных выводов и рекомендаций. В табл. 3.3 приведена структурная группировка по количественному признаку. Таблица 3.3 Группировка семей жителей С.-Петербурга по величине среднедушевого дохода (по данным за сентябрь – октябрь 1996 г.)
В данной таблице интервалы групп равны по своей величине. Если применяются равные интервалы, то расчет их величины производится по формуле где h – величина интервала, xmax и xmin – максимальные и минимальные значения признаков совокупности, k – число групп. Следует отметить, что технически удобнее иметь дело с равными интервалами, но это далеко не всегда представляется возможным из-за свойств изучаемых явлений и признаков. В экономике чаще приходится применять неравные, прогрессивно увеличивающиеся интервалы, что обусловлено самой природой экономических явлений. Применение неравных интервалов объясняется главным образом тем, что абсолютное изменение группировочного признака на одну и ту же величину имеет далеко не одинаковое значение для групп с большим и малым значением признака. Например, между двумя предприятиями с численностью рабочих до 300 человек разница в 100 человек более существенна, чем для предприятий с численностью свыше 10 000 человек. Интервалы групп могут быть замкнутыыми, когда указаны нижняя и верхняя границы, и открыгтыгми, когда указана лишь одна из границ групп. Открытые интервалы применяются только для крайних групп. При группировке с неравными интервалами желательно образование групп с замкнутыми интервалами. Это способствует точности статистических вычислений. Одна из целей статистического наблюдения – выыявле-ние связей и зависимостей между общественными явлениями. Важной задачей статистического анализа, проводимого на основе типологической группировки, т. е. в пределах однокачественных совокупностей, является задача изучения и измерения связи между отдельными признаками. Установить факт наличия такой связи позволяет аналитическая группировка. Аналитическая группировка – распространенный прием статистического изучения связей, которые обнаруживаются при параллельном сопоставлении обобщенных значений признаков по группам. Различают признаки зависимые, значения которых изменяются под влиянием других признаков, их обычно в статистике называют результативными, и факторные, оказывающие влияние на другие. Обычно в основе аналитической группировки лежит признак-фактор, а по результативным признакам производится расчет групповых средних, по изменению величины которых определяют наличие связи между признаками. Таким образом, аналитическими можно назвать такие группировки, которые позволяют установить и изучить связь между результативными и факторными признаками единиц однотипной совокупности. Важная проблема аналитических группировок – правильный выбор числа групп и определение их границ, что в последующем обеспечивает объективность характеристик связи. Поскольку анализ ведется в однокачественных совокупностях, теоретических оснований для дробления определенного типа нет, поэтому допустима разбивка совокупности на любое число групп, удовлетворяющее определенным требованиям и условиям конкретного анализа. В процессе аналитических группировок следует соблюдать общие правила группировки, т. е. единицы в образованных группах должны быть существенно различны, количество единиц в группах должно быть достаточным для расчета надежных статистических характеристик. Кроме того, групповые средние должны подчиняться определенной закономерности: последовательно увеличиваться или уменьшаться. Непосредственная группировка данных статистического наблюдения – это первичная группировка. Вторичная группировка – перегруппировка ранее сгруппированных данных. Необходимость вторичной группировки возникает в двух случаях: • ранее произведенная группировка не удовлетворяет целям исследования в отношении числа групп; • для сравнения данных, относящихся к различным периодам времени или к различным территориям, если первичная группировка была произведена по разным группи-ровочным признакам или по разным интервалам. Существует два способа вторичной группировки: • объединение мелких групп в более крупные; • выделение определенной доли единиц совокупности. В научно обоснованной группировке общественных явлений необходимо учитывать взаимозависимость явлений и возможность перехода постепенных количественных изменений в явлениях к коренным качественным изменениям. Группировка может быть научной лишь в том случае, если не только определены познавательные цели группировки, но и правильно выбрано основание группировки – группи-ровочный признак. Если группировка – это распределение на однородные группы по какому-либо признаку или объединение отдельных единиц совокупности в группы, однородные по какому-либо признаку, то группировочный признак – это признак, по которому происходит объединение отдельных единиц совокупности в отдельные группы. При выборе группировочного признака важным является не способ выражения признака, а его значение для изучаемого явления. С этой точки зрения для группировки следует брать существенные признаки, выражающие наиболее характерные черты изучаемого явления. Самая простая группировка – ряд распределения. Рядами распределения называются ряды чисел (цифр), характеризующие состав или структуру какого-либо явления после группировки статистических данных об этом явлении, другими словами, это группировка, в которой для характеристики групп применяется один показатель – численность группы. Пример использование ряда распределения приведен в табл. 3.4. Таблица 3.4 Применение рядов распределения
Приведенный ряд распределения содержит три элемента: разновидность атрибутивного признака (мужчины, женщины); численность единиц в каждой группе, называемая частотами ряда распределения; численность групп, выраженная в долях (процентах) от общей численности единиц, называемая частостями. Сумма частостей равна 1, если они выражены в долях единицы, и равна 100 %, если они выражены в процентах. Ряды, построенные по атрибутивному признаку, называют атрибутивными. Ряды распределения, построенные по количественному признаку, называются вариационныыми рядами. Числовые значения количественного признака в вариационном ряду распределения называются вариантами и располагаются в определенной последовательности. Варианты могут выражаться числами положительными и отрицательными, абсолютными и относительными. Вариационные ряды делятся на дискретные и интервальные.
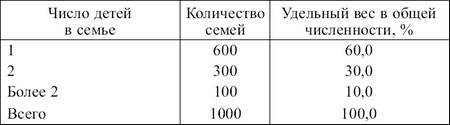
Дискретныге вариационныге рядыг характеризуют распределение единиц совокупности по дискретному (прерывному) признаку, т. е. принимающему целые значения. При построении ряда распределения с дискретной вариацией признака все варианты выписываются в порядке возрастания их величины, подсчитывается, сколько раз повторяется одна и та же величина варианта, т. е. частота, и записывается в одной строке с соответствующим значением варианта, например распределение семей по числу детей (табл. 3.5). Частоты в дискретном вариационном ряду, как и в атрибутивном, могут быть заменены частостями. Таблица 3.5 Применение дискретного ряда распределения
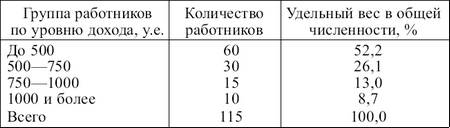
В случае непрерывной вариации величина признака может принимать любые значения в определенном интервале, например распределение работников фирмы по уровню дохода (табл. 3.6). Таблица 3.6 Случай непрерывной вариации
При построении интервального вариационного ряда необходимо выбрать оптимальное число групп (интервалов признака) и установить длину интервала. Оптимальное число групп выбирается так, чтобы отразить многообразие значений признака в совокупности. Чаще всего число групп устанавливается по формуле k = 1 + 3,32lg N = 1,44ln N + 1, где k – число групп; N – численность совокупности. Например, необходимо построить вариационный ряд сельскохозяйственных предприятий по урожайности зерновых культур. Число сельскохозяйственных предприятий – 143. Как определить число групп? k = 1 + 3,32lg N = 1 + 3,32lg143 = 8,16. Число групп может быть только целым числом, в данном случае – 8 или 9. Пример. Минимальная урожайность составляет 30 ц/га, максимальная – 70 ц/га, а число намеченных групп – 10. Величину интервала можно рассчитать по формуле (3.1): Если полученная группировка не удовлетворяет требованиям анализа, то можно произвести перегруппировку. Не следует стремиться к очень большому количеству групп, так как в такой группировке часто исчезают различия между группами. Также надо избегать образования и слишком малочисленных групп, включающих несколько единиц совокупности, потому что в таких группах перестает действовать закон больших чисел и возможно проявление случайности. Когда не удается сразу наметить возможные группы, собранный материал сначала разбивают на значительное количество групп, а затем укрупняют их, уменьшая количество групп и создавая качественно однородныле группыл.
Таким образом, группировки во всех случаях должны быть построены так, чтобы образованные в них группы как можно полнее отвечали действительности, были видны различия между группами и в одну группу не объединялись существенно различающиеся между собой явления.
|