Составы равновесных жидкости и пара
В случае совершенного раствора состояние равновесных жидкости и пара в общем случае не совпадает. На диаграмме давление-состав принято наносить точки, которые характеризуют состояние равновесного пара. Для совершенного раствора состоящего их 3-х компонентов завис. общего давления пара над раствором от состава выражается прямой линией.
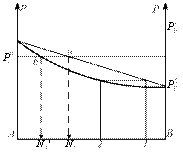
Если на эту диаграмму нанести точку выражающую состояние равновесного пара, то каждый давление. На диаграмме будут соответствовать - состояние жидкости в соответствии равновесного пара. Точка, выражающая состояние пара при различных давлениях соединяется плавной линией (линия пара). Т.о. на диаграмме 2 линии одна из которых (верхняя) характеризует состояние жидкост. раствора, она же является зависимостью общего давления пара над раствором от состояния. Эта линия называется линия жидкости. 2-ая линия (нижняя) называется линией пара и характеризует состояние равновесного пара. Чтобы определить состояние пара, находят равновесное с жидким состоянием: 1. мы должны из точки, характеризующей состояние жидкости восстановить перпендикуляр до пересечения с линией жидкости, через точку пересечения провести изобару до пересечения её с линией пара. Как видно из диаграммы в случае совершенного раствора равновесный пар всегда обогащен по сравнению с жидкостью более летучим компонентом, то есть тем компонентом, давление насыщенного пара которого выше. Линия жидкости и линия пара разделяют диаграмму на три области. Выше линии жидкости характеризуется жидким составом. Ниже линии пара – пар. Между линиями жидкости и пара характеризуется гетерогенной системой, состоящей из двух фаз – жидкости и насыщенного пара. В случае отклонения от закона Рауля линия жидкости перестаёт быть прямой, а в случае очень большого отклонения могут образовываться диаграммы с экстремами точек на линии общего давления. В реальной системе как показывает опыт, пар не всегда обогащен по сравнению с жидкостью более летучим компонентом в отношении составом равновесной жидкости и пара. Коноваловым были сформулированы два закона. Первый закон: а) повышение относительного содержания данного компонента в жидкой фазе всегда вызывает увеличение относительного содержания его в паровой фазе. б) пар более богат тем компонентом раствора, добавление которого повышает общее давление пара или понижает температуру кипения при данном давлении. Второй закон: в экстремальной точке на кривой давления пара состав пара совпадает с составом жидкости. Растворы такого состава называются постоянно кипящими или азеотропными. Законы Коновалова выводят исходя из уравнения Гиббса-Дюгема. Т/д вывод приводит к следующему выражению:
для бинарного раствора соединений компонента А и В.
т.к. Диаграммы давление-состав и температура кипения-состав
Если взять точку гетерогенной области, то она характеризует состав гетерогенной системы состоящей из жидкости и насыщенного пара. Чтобы определить состав насыщенной жидкости и пара нужно через эту точку провести изобару до пересечения её с линиями жидкости и пара. Точка в укажет на состав жидкости. Следовательно, в соответствии с первым законом Коновалова пар по сравнению с жидкостью будет более богат компонентом В. Массы равновесных фаз могут Дробная перегонка и ректификация Дистилляцией называется процесс разделения раствора на те или другие составляющие части путём перегонки. В основе метода лежит различие в составе равновесных жидкости и пара. Чем больше это различие, тем легче осуществляется разделение. Для количественной характеристики раствора в этом отношении пользуются величиной коэффициента разделения
В случае совершенных растворов коэффициент разделения не зависит от состава
|

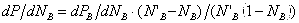
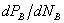 – всегда >0, т к с ростом содержания компонента В в жидкости парциальное давление его насыщенного пара может только возрасти. В экстремальной точке на линии общего давления пара
– всегда >0, т к с ростом содержания компонента В в жидкости парциальное давление его насыщенного пара может только возрасти. В экстремальной точке на линии общего давления пара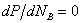 ,
,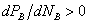 ,
, 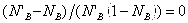 , то есть содержание компонента В в паровой фазе
, то есть содержание компонента В в паровой фазе 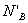 равно его содержанию в жидкости, то есть соблюдается второй закон Коновалова.
равно его содержанию в жидкости, то есть соблюдается второй закон Коновалова.
 Диаграмма давление-состав с экстремальными точками имеет вид:
Диаграмма давление-состав с экстремальными точками имеет вид: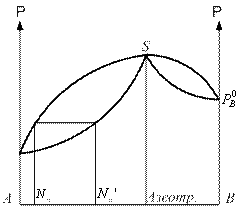 Совокупность равновесных состояний в двойной жидкостной системе может быть изображена в виде диаграммы давление-состав построенной при
Совокупность равновесных состояний в двойной жидкостной системе может быть изображена в виде диаграммы давление-состав построенной при 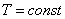 .
. выражаться в массовых долях. Состояние равновесных жидкости и пара называется сопряжёнными. Диаграмма кипение–состав напоминает обратную диаграмму давление-состав. На диаграмме кипение – состав верхняя линяя – пар, нижняя – жидкость. Через точку проводим изотерму. Можно применить правила расчёта для определения качества равновесных фаз. Диаграмма кипение-состав и давление-состав широко используются для анализа и расчёта продуктов перегонки и ректификации.
выражаться в массовых долях. Состояние равновесных жидкости и пара называется сопряжёнными. Диаграмма кипение–состав напоминает обратную диаграмму давление-состав. На диаграмме кипение – состав верхняя линяя – пар, нижняя – жидкость. Через точку проводим изотерму. Можно применить правила расчёта для определения качества равновесных фаз. Диаграмма кипение-состав и давление-состав широко используются для анализа и расчёта продуктов перегонки и ректификации. .
. . Процесс фракционной перегонки заключается в чередовании операций испарения и конденсации раствора. Процесс легко рассмотреть на примере диаграммы давление-состав или
. Процесс фракционной перегонки заключается в чередовании операций испарения и конденсации раствора. Процесс легко рассмотреть на примере диаграммы давление-состав или 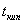 - состав использующийся законом Коновалова. Двойная система образующая диаграмму давления-состав
- состав использующийся законом Коновалова. Двойная система образующая диаграмму давления-состав 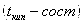 без экстремальных точек путём фракционной перегонки можно разделить на практические чистые компоненты А и В. если же диаграмма с экстремальными точками, то систему этих компонентов дробной перегонкой можно разделить либо на компонент А и азеотропный раствор, либо на компонент В и азеотропный раствор В зависимости от свойства исходных жидкостей. Процесс дробной перегонки сложен и трудоёмок в промышленном масштабе. Разделение удаётся осуществить более успешно, проводя перегонку в форме непрерывного процесса, в котором операции конденсации и дистилляции отдельных фракций автоматизированы - ректификация. Разделение зависит от 3 факторов: 1) коэффициент разделения который свойственен данному раствору и зависимость его от состава в данной системе 2) от числа тарелок в колонне 3) от эффективности работы каждой тарелки.
без экстремальных точек путём фракционной перегонки можно разделить на практические чистые компоненты А и В. если же диаграмма с экстремальными точками, то систему этих компонентов дробной перегонкой можно разделить либо на компонент А и азеотропный раствор, либо на компонент В и азеотропный раствор В зависимости от свойства исходных жидкостей. Процесс дробной перегонки сложен и трудоёмок в промышленном масштабе. Разделение удаётся осуществить более успешно, проводя перегонку в форме непрерывного процесса, в котором операции конденсации и дистилляции отдельных фракций автоматизированы - ректификация. Разделение зависит от 3 факторов: 1) коэффициент разделения который свойственен данному раствору и зависимость его от состава в данной системе 2) от числа тарелок в колонне 3) от эффективности работы каждой тарелки.


