Порядок работы. 1. Рассчитать оптимальный размер партии поставки аналитическим и графическим методом, годовой объем потребления продукции Q
1. Рассчитать оптимальный размер партии поставки аналитическим и графическим методом, годовой объем потребления продукции Q, тариф на перевозку одной партии 2. Рассчитать оптимальный размер партии в условиях дефицита при величине расходов, связанных с дефицитом Расчет ведется по исходным данным для варианта 0. Пример 1. Оптимальный размер партии поставки С определяется по критерию минимума суммарных затрат на транспортировку продукции и хранение запасов. Величина суммарных затрат рассчитывается по формуле
С=Стр+Схр (2.1)
где Стр — затраты на транспортировку за расчетный период (год), руб.; Схр — затраты на хранение запаса за расчетный период (год), руб.
Величина Стр определяется по формуле Стр=n·стр (2.2)
где n — количество партий, доставляемых за расчетный период; стр — тариф на перевозку одной партии, руб/партия.
n= где g – размер партии.
Затраты на хранение определяются по формуле
Схр= g ср ∙ схр, (2.4)
где g ср – средняя величина запаса (в тоннах), которая определяется из предположения, что новая партия завозится после того, как предыдущая полностью израсходована.
В этом случае средняя величина рассчитывается по формуле g ср = g /2 (2.5)
Подставив выражения Стр и Схр в формулу (2.1), получим
С=
Функция общих затрат С имеет минимум в точке, где ее первая производная по g равна нулю, т.е.
Решив уравнение (2.7) относительно g, получим оптимальный размер партии поставки (формула Уилсона) [1, с.114] или[4, с.504]:
g =
Подставив заданные значения, получим
g =
При этом общие затраты составят
С =
Решение данной задачи графическим способом заключается
Таблица 2.3 – Значения затрат на транспортировку Стр, на хранение Схр, и суммарных затрат С
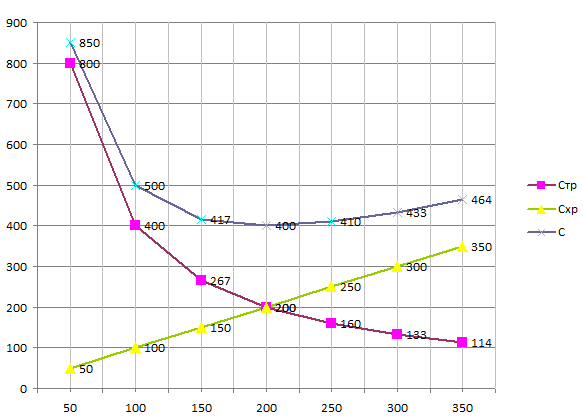
По данным таблицы 2.3 построены графики зависимости затрат на транспортировку, хранение и суммарных от размера партии
Рисунок 2.1 – Графики зависимости затрат от размера партии
Анализ графиков на рисунке 2.1 показывает, что затраты на транспортировку уменьшаются с увеличением размера партии, что связано с уменьшением количества рейсов. Затраты, связанные График суммарных затрат имеет минимум при значении g, приблизительно равном 200 т, которое и является оптимальным значением размера партии поставки. Соответствующие минимальные суммарные затраты составляют 400 руб.
2. В условиях дефицита значение g, рассчитанное по формуле (2.8), корректируется на коэффициент Коэффициент
Подставив значения, получим
Из этого следует, что в условиях возможного дефицита размер оптимального значения партии при заданных данных необходимо увеличить на 29%. Вывод
Рассчитан оптимальный размер партии поставки аналитическим и графическим методом, получен общий результат: оптимальный размер партии 200 т, при общих затратах 400 руб., также произведен расчет
Контрольные вопросы 1. Укажите, какие факторы влияют на оптимальную частоту завоза грузов. 2. Перечислите существующие критерии оптимальности. 3. Поясните, от чего зависят расходы по доставке и хранению. 4. Объясните, что происходит с расходами по доставке грузов при увеличении размера заказа. Какими партиями осуществляются перевозки и как часто. 5. Расскажите, что происходит с расходами по хранению, если заказ увеличивается.
Содержание отчета 1. Рассчитать оптимальный размер партии поставки грузов аналитическим методом (по формуле Уилсона). 2. Рассчитать оптимальный размер партии поставки грузов графическим методом и построить график. 3. Произвести расчеты коэффициента k. 4. Математические расчеты сверить с компьютерной версией. Практическое занятие № 3 «Определение оптимального места расположения склада на заданном полигоне» (2 часа) Цель:
Научиться определять расположение склада на полигоне.
Склады – это здания, сооружения и разнообразные устройства, предназначенные для приемки, размещения и хранения поступивших на них товаров, подготовки их к потреблению и отпуску потребителю. Склады являются одним из важнейших элементов логистических систем. Одной из основных задач, реш а емых в процессе создания складской системы, является определение месторасположения (дислокации) складов в определенной территориальной зоне. Для оптимальной дислокации складов требуются достаточно сложные экономико-математические методы и модели. Одним из наиболее простых методов определения географического месторасположения склада является метод «сетки», ориентированный на определение объекта с минимальными транспортными расходами, связанными
Таким образом, при обосновании решения о формировании складской сети и определения дислокации складов следует руководствоваться двумя основными критериями: · Минимальными совокупными затратами, связанными · Максимальным уровнем обслуживания потребителей.
Рациональное размещение складского хозяйства существенно влияет на общие размеры грузопотоков и способствует сокращению транспортных и складских затрат [1, с.88], [4, с.595].
|

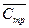 , расходы, связанные
, расходы, связанные  принять по исходным данным.
принять по исходным данным.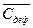 .
.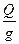 , (2.3)
, (2.3) c тр +
c тр + 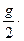 c хр (2.6)
c хр (2.6)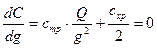 (2.7)
(2.7) (2.8)
(2.8) =200 т.
=200 т.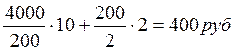 .
.
 , учитывающий расходы, связанные с дефицитом.
, учитывающий расходы, связанные с дефицитом. рассчитывают по формуле
рассчитывают по формуле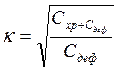 (2.9)
(2.9)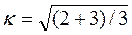 =1,29; g =1,29·200=258 т в условиях дефицита.
=1,29; g =1,29·200=258 т в условиях дефицита.


