Прохождене частицы через потенциальный барьер
Пусть микрчастица движется в пространстве по оси Х. По характеру изменения величины потенциального поля пространство по по оси Х можно разбить на три области (рис. 2): I. Х ≤ 0, U =0; II. 0 ≤ Х ≤ d, U=U; III. X ≥ d, U = 0
Для области II:
Для областей I и III показатели экспоненты комплексные и волновая функция остается гармонической, но с разными амплитудами А1 > А3. Характер движения частицы в области II зависит от значения ее кинетической энергии и величины U. Наиболее интересно поведение частицы при Е < U. При этом условии
Показатель Ψ2(х) является действительным и в области II волновая функция затухает по экспоненте (рис. 2). Вероятность обнаружить частицу на правой границе потенциального барьера, т.е. при х = d равна |Ψ2(d)|2 А вероятность D того, что частица пройдет потенциальный барьер, определяется отношением D = Величину D называют прозрачностью барьера. И как бы не была велика величина U, существует конечная вероятность того, что микрочастица пройдет через потенциальный барьер. С точки зрения классической механики, если энергия частицы меньше высоты потенциального барьера E < U, то она его принципиально преодолеть не может. Итак, существует вероятность того, что частица может пройти, туннелировать через потенциальный барьер U без потери своей энергии Е даже при E < U. Такое прохождение частицы называется туннельным эффектом и является чисто квантовым явлением, связанным с волновыми свойствами микрочастицы. Туннельный эффект находит широкое применение в микроэлектронике, в частности в туннельных p-n-переходах.
|

 Подобное изменение потенциального поля называют потенциальным барьером. Для указанных областей решения уравнения Шредингера согласно (9) и (10) можно записать в следующем виде: для областей I и III:
Подобное изменение потенциального поля называют потенциальным барьером. Для указанных областей решения уравнения Шредингера согласно (9) и (10) можно записать в следующем виде: для областей I и III: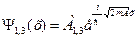
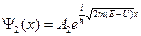
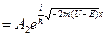


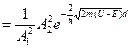 ≈
≈ 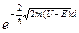 (11)
(11)


