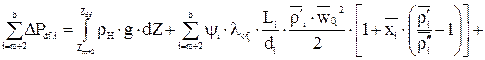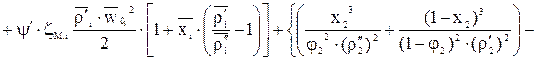Розв’язання
Обчислимо коефіцієнти і праві частини систем (5.6) і (5.7):
Для багаточлена першого ступеня система має вигляд
Розв’язавши таку систему рівнянь отримаємо функцію першого степеня Ф(х) = -25,92 + 1,012 × х – див. рис. 5.1, в. Аналогічно для функції другого степеня система виглядатиме
Розв’язання такої системи відносно коефіцієнтів полінома дозволить отримати таку апроксимуючу функцію Ф(х) = 12,74 – 0,921 × х + 0,0175 × х2. (див. рис. 5.1, а). Середньоквадратичне відхилення для обох випадків складе
Задачі для самостійної роботи Приклад 5.4. Виконати лінійну та квадратичну інтерполяцію термодинамічної властивості насиченої водяної пари при температурі 205°С і порівняти із довідковим значенням.
Варіант 1
Варіант 2
Варіант 3
Приклад 5.5. Використовуючи метод найменших квадратів, апроксимувати багаточленом першого та другого степенів залежність термодинамічної властивості води на лінії насичення від температури. Варіант 1
Варіант 2
Варіант 3
6 КЛАСИФІКАЦІЯ МАТЕМАТИЧНИХ МОДЕЛЕЙ
6.1 Постановка задачі Формальна класифікація моделей ґрунтується на класифікації математичних засобів, що використовуються. Часто будується у формі дихотомій. Наприклад, один з популярних наборів дихотомій: - лінійні або нелінійні моделі; - детерміновані або стохастичні; - зосереджені або розподілені системи; - статичні або динамічні; - структурні та функціональні; - дискретні або безперервні і так далі. Природно, що можливі і змішані типи: в одному відношенні зосереджені (по частині параметрів), в іншому - розподілені моделі і т.д.
6.2 Класифікація моделей в залежності від параметрів моделі
В залежності від основних параметрів математичні моделі можна класифікувати на групи (див. рис. 6.1). 6.3 Класифікація моделей за змістовною побудовою
Структурні моделі представляють об'єкт як систему з своєю структурою і механізмом функціонування. Функціональні моделі не використовують таких уявлень і відображають тільки ззовні сприйману поведінку (функціонування) об'єкту. В їх граничному виразі вони називаються також моделями «чорної скрині». В такому випадку описують з відомою точністю зв’язок між входами X і виходом Y системи на основі експериментальних даних без аналізу внутрішньої структури системи, яку можна розглядати як “чорну скриню”. Модель відрізняється універсальністю методології збирання експериментальної інформації і будови моделей. До недоліків варто віднести складність різносторонньої інтерпретації параметрів моделей і обмеженість області їх дії з відповідною точністю рамок тих конкретних об’єктів, для яких вони побудовані. Можливі також комбіновані типи моделей, які іноді називають моделями «сірої скрині». Практично всі автори, що описують процес математичного моделювання, указують, що спочатку будується особлива ідеальна конструкція, змістовна модель. Термінології, що встоялася, тут немає, і інші автори називають цей ідеальний об'єкт концептуальна модель, умоглядна модель або предмодель. При цьому фінальна математична конструкція називається формальною моделлю або просто математичною моделлю, отриманою в результаті формалізації даної змістовної моделі (предмоделі). Побудова змістовної моделі може проводитися за допомогою набору готових ідеалізацій, як в механіці, де ідеальні пружини, тверді тіла, ідеальні маятники, пружні середовища і т.п. дають готові структурні елементи для змістовного моделювання. Проте в областях знання, де не існує повністю завершених формалізованих теорій (передній край фізики, біології, економіки, соціології, психології, і більшості інших областей), створення змістовних моделей різко ускладнюється. Перш за все будують деяку інженерну концептуальну модель, яка виражається на початку словами в термінах даної науки (матеріалознавство, технологія). Ця концептуальна модель описується далі абстрактно-знаково за допомогою диференціальних або алгебраїчних рівнянь, геометричних співвідношень, логічних операцій тощо. В основі математичної моделі лежить уява про те, що поведінка реального об’єкту аналогічна поведінці концептуальної моделі. Перевага моделі полягає у наочності “фізичної” інтерпретації об’єкта. Недолік полягає в тому, що описати математичними символами можна концепцію, яка далека від реальності.
6.4 Класифікація моделей в залежності від мети моделювання
Метою дескриптивних моделей (від лат. descriptio - опис) є встановлення законів зміни параметрів моделі. Приклад дескриптивної моделі – модель теплової схеми теплоенергетичного чи теплотехнологічного об’єкту. Параметри моделі – теплові потужності, температурні графіки протягом року (вхідні), температури і витрати теплоносіїв в елементах схеми (власні параметри). Кінцевими параметрами будуть потужності генерувального обладнання, витрати палива та коефіцієнт корисної дії установки в довільний момент часу. Оптимізаційні моделі призначені для визначення оптимальних (якнайкращих) з погляду деякого критерію параметрів модельованого об'єкту або ж для пошуку оптимального (якнайкращого) режиму управління деяким процесом. Як правило, дані моделі будуються з використанням однієї або декількох дескриптивних моделей і включають деякий критерій, що дозволяє порівнювати різні варіанти наборів значень кінцевих параметрів між собою з метою вибору якнайкращого. На область значень вхідних параметрів можуть бути накладений обмеження у вигляді рівності і нерівностей, пов'язані з особливостями даного об'єкту або процесу. Прикладом оптимізаційної моделі може служити моделювання конструкції теплотехнологічного апарату, наприклад, теплообмінника із мінімальними витратами під час його створення та експлуатації за умов визначеної теплової потужності. Відзначимо, що для більшості реальних процесів, конструкцій потрібне визначення оптимальних параметрів відразу по кількох критеріях, тобто ми маємо справу з так званими багатогокритериальными задачами оптимізації. При цьому нерідкими є ситуації суперечності критеріїв. Управлінські моделі застосовуються для ухвалення ефективних управлінських рішень в різних областях цілеспрямованої діяльності людини. Проте на практиці під ухваленням рішень звичайно розуміється вибір деяких альтернатив із заданої їх множини, Наприклад, на підприємстві звільнилася посада головного інженера і задача директора полягає у виборі з наявної безлічі кандидатів на цю посаду одного, що відповідає заданим вимогам. Складність задачі полягає в наявності невизначеності як за початковою інформацією (неповні дані про кандидатів) і характеру дії зовнішніх умов (випадкове: вибраний кандидат захворів або відмовився; ігрове: міністерство проти вибраної кандидатури), так і по меті (суперечливі вимоги до вибираної кандидатури: повинен бути добрим фахівцем і адміністратором, досвідчений, енергійний, молодий і ін.).
6.5 Класифікація математичних моделей залежно від методів реалізації Метод реалізації моделі відносять до аналітичних, якщо він дозволяє отримати вихідні параметри у вигляді аналітичних виразів, тобто виразів, в яких використовується не більше ніж рахункова сукупність арифметичних операцій і переходів до межі. Аналітичні моделі поділяють на алгебраїчні та наближені. В алгебраїчних моделях використовується кінцеве число арифметичних операцій, операцій зведення в цілочисельний ступінь і визначення кореня. Дуже часто аналітичне рішення для моделі представляють в елементарних або спеціальних функціях: показових, логарифмічних, тригонометричних, гіперболічних і т.п. Для отримання значень цих функцій при конкретних значеннях вхідних параметрів використовують їх розкладання в ряди (наприклад, Тейлора). Враховуючи різне число членів ряду, можна обчислювати значення функції з різним ступенем точності. Моделі, що використовують подібний прийом, називаються наближеними. Аналітичні методи реалізації моделі є більш цінними в тому плані, що дозволяють з меншими обчислювальними витратами вивчити властивості об'єкту моделювання застосовуючи традиційні добре розвинуті математичні методи аналізу аналітичних функцій. Істотно, що застосування аналітичних методів можливо без використовування ЕОМ (за винятком випадків коли аналітичне рішення визначається в рядах і для його доведення до числа потрібні трудомісткі обчислення із застосуванням ЕОМ). Крім того знання аналітичного виразу для шуканих параметрів дозволяє досліджувати фундаментальні властивості об'єкту, його якісну поведінку, будувати нові гіпотези про його внутрішню структуру. Слід зазначити що можливості аналітичних методів істотно залежать від рівня розвитку відповідних розділів математики. На даний час могутній сплеск інтересу до аналітичних методів при реалізації моделей пов'язаний з появою пакетів математичних обчислень (Derive, MatLab, Mathcad, Maple, Mathematica, Scientific Workplace і ін.). Застосування подібних програмних засобів не тільки спрощує процедуру отримання аналітичного рішення, але і полегшує подальший аналіз отриманого рішення із застосуванням різного роду візуализаторів. На жаль, існуючі в даний час математичні методи дозволяють отримати аналітичні рішення тільки для відносно нескладних математичних моделей у вузькому діапазоні значень параметрів. В більшості випадків при дослідженні моделей доводиться використовувати алгоритмічні підходи, що дозволяють отримати лише наближені значення шуканих параметрів. Алгоритмічні моделі поділяють на чисельні та імітаційні. При чисельному підході сукупність математичних співвідношень моделі замінюється кінцевомірним аналогом. Це частіше за все досягається дискретизацією початкових співвідношень, тобто переходом від функцій безперервного аргументу до функцій дискретного аргументу. Знайдене рішення дискретної задачі ухвалюється за наближене рішення початкової математичної задачі. Основною вимогою до обчислювального алгоритму є необхідність отримання рішення початкової задачі із заданою точністю за кінцеве число кроків. Якщо при чисельному підході дискретизації піддавалася отримана система математичних співвідношень, то при імітаційному підході на окремі елементи розбивається сам об'єкт дослідження. В цьому випадку система математичних співвідношень для об'єкту-системи в цілому не записується, а замінюється деяким алгоритмом, що моделює її поведінку і що враховує взаємодію один з одним моделей окремих елементів системи. Моделі окремих елементів можуть бути як аналітичними, так і алгоритмічними. Безперечною перевагою алгоритмічних моделей є відсутність принципових обмежень на складність моделі, що дозволяє застосовувати їх для дослідження систем довільної складності.
Контрольні запитання
1. Поясніть відмінність структурної та функціональної моделі. 2. Поясніть відмінність змістовної та формальної моделі. 3. Поясніть особливості моделей типу "чорної скрині". 4. Дайте класифікацію моделей з невизначеними параметрами і змінними моделювання. 5. Дайте класифікацію моделей за змінністю параметрів в часі. 6. Дайте класифікацію моделей відносно складу параметрів. 7. Поясніть відмінність управлінських, оптимізаційних та дескриптивних моделей. 8. Поясніть відмінність аналітичних та алгоритмічних моделей.
7 ЕТАПИ МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ
7.1 Етапи побудови моделі
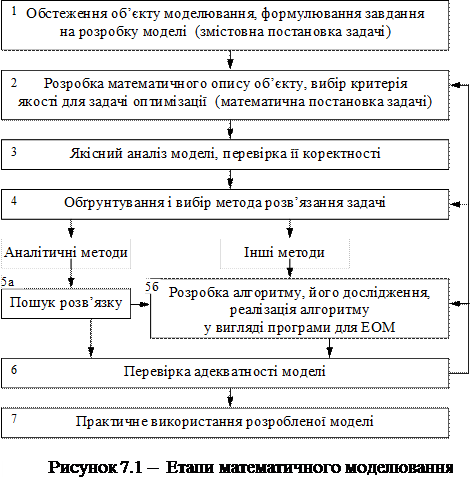
Процес створення математичних моделей трудомісткий, довготривалий і пов’язаний з використанням висококваліфікованої праці. Особливістю математичних моделей, створюваних в даний час, є їх комплексність, пов’язана з складністю модельованих об'єктів. Наприклад при моделюванні процесів деформування різних конструкцій під дією прикладеного навантаження доводиться враховувати не тільки процеси масо переносу, що відбуваються при деформуванні, але і теплоперенос, а також пов’язані з цим процеси. На даний час характерне представлення об’єкту моделювання у вигляді складної системи взаємодіючих елементів. Все це приводить до ускладнення моделі і необхідності сумісного використовування декількох теорій, застосування сучасних обчислювальних методів і обчислювальної техніки. Впровадження обчислювальної техніки у всі сфери діяльності привело до повсюдного використання математичних моделей. Зауважимо, що ЕОМ — це тільки «залізо», а «розумним» і корисним його роблять програми, які в більшості випадків є реалізаціями алгоритмів відповідних математичних моделей. У разі складних об'єктів задовольнити всім вимогам, що пред'являються, в одній моделі звичайно неможливо. Доводиться створювати цілий спектр моделей одного і того ж об’єкту (в деяких випадках – ієрархічну сукупність «вкладених» одна в іншу моделей). Для зменшення витрат розробку моделей і імовірності виникнення помилок розроблений алгоритм створення математичних моделей (рис. 7.1).
7.2 Обстеження об’єкту моделювання
Основним завданням обстеження об’єкту є підготовка змістовної постановки задачі моделювання. Змістовна постановка задачі – це перелік сформульованих у змістовній (словесній) формі основних питань, на які повинна відповідати розроблена модель, опис її основних характеристик. В реальних умовах на цьому етапі необхідно зібрати великий об’єм інформації і потім з цього об’єму мало формалізованої різноманітної інформації, з нечітко поставлених та сформульованих побажань виділити такі вимоги, які з одного боку задовольняють замовника, з іншого – дозволяють реалізувати модель у визначені терміни і в рамках виділених матеріальних засобів. Для вирішення такого завдання необхідні спеціалісти, що знають можливості та обмеження обчислювальних машин.
Під час обстеження об’єкту виконують такі завдання: – виявлення основних факторів, механізмів, що впливають на поведінку об’єкта, методів визначення параметрів, що описують об’єкт; – збір і перевірка наявної експериментальної інформації про об’єкти-аналоги, проведення при необхідності додаткових експериментів; – аналітичний огляд наявної літературної та іншої інформації, аналіз розроблених раніше моделей даного об’єкту або подібного; аналіз та узагальнення всього накопленого матеріалу, розробка загального плану створення моделі. З використанням накопленого матеріалу виконують змістовну постановку задачі. Звичайно в подальшому можуть вноситись доповнення, але вони повинні носити частковий, непринциповий характер. Змістовна постановка задачі може бути оформлена у вигляді технічного завдання на розробку моделі. Етап створення технічного завдання може займати до 30 % часу, відпущеного на розробку моделі.
7.3 Математична постановка задачі
На даному етапі виконується спочатку концептуальна постановка задачі – сформованих у термінах певної науки (фізики, хімії, біології тощо) перелік основних питань, що повинна вирішувати модель, а також сукупність гіпотез відносно властивостей і поведінки об’єкта моделювання. Концептуальна модель будується як ідеалізована модель об’єкта. Згідно з прийнятими гіпотезами визначається набір параметрів, що описують стан об’єкта, та перелік законів, що описують поведінку об’єкта, взаємозв’язок між параметрами та об’єкта із навколишнім середовищем. Важливою складовою концептуальної моделі є вибраний критерій якості об’єкту. Призначення критерію – встановлення переважного варіанта виконання об’єкта в задачах оптимізації. Для масових оптимізаційних задач в системах, що знаходяться на нижніх ієрархічних рівнях, в якості критерія оптимальності обирають мінімум зведених витрат. Це показник, що враховує первинні та експлуатаційні витрати в грошових показниках. Поряд з таким критерієм розглядають і додаткові – екологічні обмеження, перспективність прийнятих рішень з врахуванням технічного прогресу, підвищення продуктивності праці тощо. Чим вищий рівень системи тим більший вплив мають саме додаткові критерії. Математична постановка задачі (математичний опис об’єкта) – це сукупність математичних співвідношень, що описують поведінку об’єкта моделювання. Найбільш простий математичний опис складається з алгебраїчних рівнянь. Але область застосування таких моделей дуже обмежена. Для створення моделей складних систем використовують знання, що сконцентровані у аксіомах, теоремах, законах, що мають чітке математичне формулювання. Відокремлюють закони, справедливі для всіх типів задач і співвідношення, що описують поведінку окремих об’єктів. До першого класу відносяться, наприклад, закони збереження маси, кількості руху і енергії. До другого – співвідношення між параметрами у вигляді рівнянь стану, наприклад, закон Гука, Клапейрона, Стефана-Больцмана та ін. Співвідношення другого класу мало вивчені, іноді навіть необхідно розробляти власні замикаючі співвідношення, наприклад, по інтенсивності тепловіддачі в певних умовах тощо. В більшості випадків математичний опис об’єкту включає звичайні диференційні рівняння, особливо для динамічних моделей, диференційні рівняння у частинних похідних, інтегродиференційні рівняння тощо. Обов’язковим елементом математичної постановки задачі є прийняті допущення і спрощення при побудові моделі.
7.4 Якісний аналіз моделі, перевірка коректності
Для контролю правильності складного математичного опису необхідно виконати ряд перевірок: – контроль розмірностей (прирівнюватись і додаватись можуть лише величини з однаковими розмірностями, в однаковій системи одиниць); – контроль порядків (при додаванні величин виконується грубе їх порівняння і малозначимими складовими можна нехтувати); – контроль характеру залежностей і фізичного змісту; – контроль екстремальних ситуацій (перевірка поводження моделі при досяганні параметрами меж допустимого діапазону (нуль або нескінченність)); – контроль граничних умов; – контроль математичної замкнутості (перевірка чи має система математичних виразів однозначний розв’язок), тобто перевірка "коректності математичної задачі". Математична модель називається коректною, якщо для неї успішно виконані всі вищенаведені контрольні перевірки.
7.5 Обґрунтування і вибір методу розв’язання задачі
Вибір того чи іншого метода в великій мірі залежить від кваліфікації спеціалістів. Аналітичні методи більш зручні для аналізу результатів, але можуть бути застосовані лише для відносно простих моделей. Алгоритмічні методи більш трудомісткі, вимагають знання обчислювальної математики, програмних комплексів, потужної техніки. Точність таких методів залежить від вибору метода і параметрів, наприклад, кроку інтегрування. Використання будь-якого аналітичного методу призводить до виникнення похибки: похибки вихідних даних; похибки методу; похибки округлення. Підбір метода повинен забезпечувати ефективність (мінімум часу за достатньої точності), стійкість точність результатів.
7.6 Реалізація моделі у вигляді програми
Процес розробки програмного продукту на основі розробленої моделі є не менш складним і важливим, ніж попередні етапи. Процес створення програмного забезпечення складається з етапів: – складання технічного завдання на розробку пакета програм; – проектування структури програмного комплексу; – кодування алгоритму; – тестування та відлагодження; – супровід та експлуатація. Найбільш ефективним варіантом є розбивання програми на окремі модулі. Для кожного модуля складається алгоритм, що дозволяє виконувати відповідні функції. Розробляється система зв’язків між модулями яка називається схемою потоків даних програмного комплексу. Більшість програм має три елементи: – препроцесор – система підготовки і перевірки початкової інформації; – процесор – розв’язання задачі, реалізація обчислень; – постпроцесор – відображення отриманих результатів. Як правило створення моделі та програмного комплексу може займати 3…5 років. Якісні, надійні, із зручним інтерфейсом програми можна створювати лише за умов використання сучасних методів структурного, абстрактного, об’єктно-орієнтованого і візуального програмування. Розробка бібліотек прикладних програм для розв’язання окремих задач з уніфікованими форматами передачі даних дозволяє значно скоротити час розробки програми.
7.7 Перевірка адекватності моделі
Під адекватністю моделі розуміють ступінь відповідності результатів, отриманих з використанням розробленої моделі даним експерименту або тестової задачі. Перевірка адекватності має на меті: – впевнитись в справедливості прийнятої сукупності гіпотез на етапі концептуальної і математичної моделі; – встановити, що точність отриманих результатів відповідає точності, вказаної в технічному завданні. В моделях для виконання оціночних розрахунків задовільною вважається похибка 10…15%. В моделях, що використовуються в керуючих і контролюючих системах допустима похибка 1…2% і менше. Неадекватність результатів можлива з трьох причин: – значення заданих параметрів моделі не відповідають допустимій області цих параметрів; – прийнята система гіпотез вірна, але константи і параметри у визначальних співвідношеннях не встановлені достатньо точно; – невірна використана система гіпотез. При неадекватності результатів необхідно провести коректування моделі, розглядаючи причини у вищенаведеній послідовності.
7.8 Практичне використання розробленої моделі
Дескриптивні моделі призначені для опису досліджуваних параметрів процесу, а також для дослідження закономірностей зміни цих параметрів. Вони використовуються для: – вивчення властивостей та особливостей поведінки об’єкту при різних наборах початкових даних і різних режимах; – як моделюючі блоки в різних САПР та АСУ; – при побудові оптимізаційних моделей і моделей-імітаторів. Дослідницькі моделі використовуються тільки під час виконання дослідницьких робіт, вони, переважно, не мають зручного інтерфейсу, але використовують найбільш прогресивні процедури і алгоритми. Моделі і побудовані на їх основі програмні комплекси повинні мати зручний інтерфейс, потужні пре- і постпроцесори, детальні і якісно складені рекомендації по використанню. Як правило, вони не можуть бути модернізовані і вдосконалені.
Контрольні запитання 1. Поясніть алгоритм створення математичної моделі. 2. Охарактеризуйте етап змістовної постановки задачі при розробці математичної моделі. 3. Поясніть відмінність концептуальної і математичної постановки задачі. 4. Поясніть що таке критерій якості об’єкту, наведіть приклади. 5. Охарактеризуйте різновиди контрольних перевірок моделі. 6. Поясніть вимоги при виборі методу розв’язання задачі. 7. Проаналізуйте етапи створення програмного продукту і його складові. 8. Призначення перевірки адекватності моделі і причини її неадекватності.
8 МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ В РАМКАХ ДИПЛОМНОГО ПРОЕКТУВАННЯ
8.1 Системний підхід до досліджень
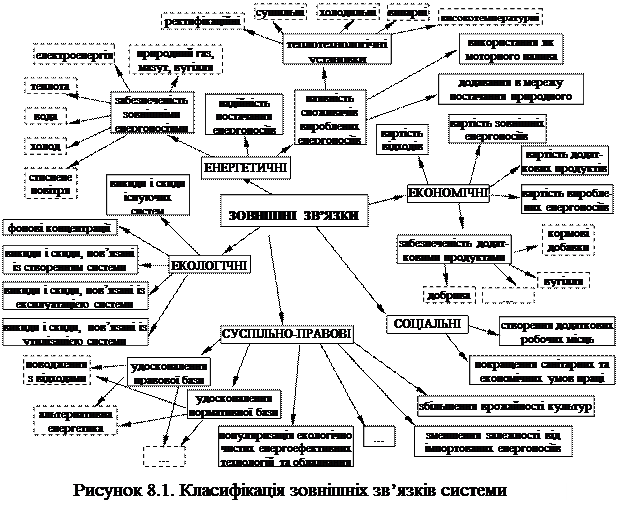
Теплоенергетичні об’єкти є складними за своєю структурою та елементною базою. Якісне математичне моделювання таких об’єктів неможливе системного підходу, який дозволяє спростити одну з найскладніших проблем моделювання – велику розмірність задачі. Теплоенергетична установка є складовою системи більш високого рівня і в свою чергу складається з систем нижчого ієрархічного рівня. На даному етапі системний підхід неможна розглядати як сукупність чітких правил, використовуючи які можна розв’язувати складні задачі. Але є певні етапи для задачі оптимізації складної системи. Виділення досліджуваного теплоенергетичного об’єкта з більш загальної системи. Наприклад, котельні з системи теплопостачання міста. Необхідно чітко окреслити межі об’єкта, мету оптимізації та критерій оптимальності. Виявлення складу елементів об’єкту та взаємозв’язків між ними. Тобто розробити ієрархію елементів об’єкта. Агрегування реальних елементів і зв’язків об’єкту. Результатом є складання ієрархічної системи окремих елементів об’єкту і їх зв’язків, які є доступними для дослідження. Формулювання набору задач для кожного елемента, що дозволить вирішити основну задачу оптимізації теплоенергетичного об’єкта. Формулювання інформаційних зв’язків між елементами об’єкта, за допомогою яких вони обмінюються початковими та проміжними даними, та іншими показниками. Розробка комплексу моделей елементів об’єкта, за допомогою якого можливо проводити комплексну оптимізацію об’єкта. Кожен теплоенергетичний об’єкт має зовнішні зв’язки, наприклад, вид палива, його характеристики та умови постачання, забезпеченість системами водопостачання, кліматичні умови, місце розташування, можливості металургії, хімії, машинобудування, стан економіки наявність трудових ресурсів та ін. З усього вищенаведеного зрозуміла вся складність та різноманітність впливу зовнішніх зв’язків об’єкта. Зворотна зовнішня інформація може включати такі показники: – техніко-економічні показники, інвестиції, питомі капіталовкладення тощо; – технологічні, масогабаритні показники, що впливають на виготовлення, транспортування, монтаж тощо; – шкідливі викиди та скиди, пов’язані із виготовленням, транспортуванням, монтажем та експлуатацією об’єкта.
Крім зовнішніх зв’язків значний вплив на набір елементів та схемне оформлення спричиняють внутрішні інформаційні зв’язки: властивості теплоносіїв; закономірності технологічних процесів, конструктивні та схемні характеристики елементів об’єкта тощо.
8.2 Методика побудови математичних моделей
Для складання моделі теплоенергетичний об’єкт розглядається як характерна ланка енергогенерувальної системи з одного боку, і як складний комплекс різнорідних елементів обладнання та споруд, з’єднаних зв’язками. Теплові схеми об’єктів можуть моделюватись за допомогою теорії графів, або іншими методами. В теорії графів елементи обладнання є вершинами, які зв’язані дугами – лініями трубопроводів. Основою математичної моделі теплоенергетичного об’єкта є система балансових рівнянь для всієї системи та її кожного елемента: – рівняння балансу енергії
– рівняння балансу витрат
– рівняння гідравлічного і аеродинамічного балансів
– рівняння зміни ентальпії в елементі теплоенергетичного об’єкту
Між параметрами об’єкта та його елементами існують достатньо складні зв’язки. Для зменшення розмірності задачі обирають найважливіші характеристики елементів, опис взаємозалежностей між якими дозволяє з достатньою точністю моделювати об’єкт. Основними характеристиками теплоенергетичного об’єкту є: – характеристики зміни тиску енергоносіїв; – характеристики зміни ентальпії енергоносіїв; – характеристики середньої швидкості енергоносіїв; – характеристики найбільшої температури стінки елемента тощо. Будь-яка модель теплоенергетичного об’єкту має ряд обмежень. Термодинамічні, витратні, конструктивні та інші параметри не можуть приймати довільні значення. Вони завжди знаходяться в межах фізично можливих і технічно здійснених станів енергоносіїв та обладнання. Прикладом таких обмежень є товщини стінок елементів, термодинамічні властивості енергоносія, довжина топки (з умови розповсюдження полум’я), при дефіцитності якогось матеріалу обмеженням може бути витрата цього матеріалу тощо. В якості функції мети – критерію оптимальності – найчастіше використовують показник «приведені витрати». Обов’язковим правилом порівняння варіантів є приведення їх до однакового енергетичного ефекту, наприклад, однакової потужності.
8.3 Розробка математичного опису теплогідродинамічних процесів у дренажному каналі
Дренажними каналами (ДК), що реалізуються у теплотехнологічних схемах підприємств, є, як правило, довгі канали, що працюють в області невисокого тиску. У більшості дренажних систем ми можемо спостерігати критичні потоки. Найчастіше дренажні канали це досить складні системи, що містять значну кількість місцевих опорів, які можуть не мати між собою ділянок, достатніх для стабілізації потоку. Під час формування математичної моделі теплогідродинамічних процесів у ДК задача витікання розглядається у одновимірній постановці для встановленого режиму течії. Рідина приймається ньютонівською і однорідною. Параметри її стану на кривій насичення однозначно визначаються величиною тиску вздовж каналу витікання і описуються рівнянням Клайперона–Клаузіуса. Температура пари вважається рівною температурі насичення при відповідному тискові потоку, а зміна її стану підпорядковується законам реального газу. Модель баротропна, тобто тиски рідини і пари по обидві сторони міжфазної поверхні розділу рівні. Теплофізичні властивості обох фаз встановлюються за довідковими даними. В задачі враховувався теплообмін між фазами, а також між потоком і стінкою каналу, а також втрати енергії на тертя об стінки каналу. Задача розв’язувалась з врахуванням фазового перетворення рідина-пара (випаровування). Основою рішення задачі є фундаментальні закони збереження маси і повної енергії для двофазного потоку, а також деякі фізично обґрунтовані замикаючі співвідношення. Зважаючи на особливості процесів, що відбуваються під час течії самозакипаючої рідини у дренажному каналі, математичну модель доцільно розділити на блоки, що описують конкретний процес, а саме: 1) розрахунок гідродинамічних процесів; 2) розрахунок тепломасообмінних процесів; 3) розрахунок параметрів критичної течії. Набір закономірностей, що включають у себе відповідні блоки залежить від набору початкових параметрів, які визначають режим течії та умови протікання процесів у дренажному каналі. Блок розрахунку гідродинамічних процесів має включати в себе рівняння для визначення втрат тиску на тертя, в місцевих опорах, на прискорення та нівелірної складової. Блок розрахунку тепломасообмінних процесів включає в себе відомі залежності теплових і матеріальних балансів та рівняння теплопередачі. Блок розрахунку параметрів критичної течії містить залежності для визначення швидкості розповсюдження слабких збурень у двофазному потоці та критичного тиску. Доповнивши вищенаведені блоки залежностями для визначення теплофізичних властивостей води та пари, отримаємо математичну модель руху самозакипаючої рідини у дренажному каналі. Для побудови математичної моделі ДК розбиваємо на ділянки (b ділянок) зі сталим діаметром (d = const). Кожна і-та ділянка із b ділянок має в загальному випадку: довжину Lі; ni місцевих опорів, кожен з яких характеризується умовним коефіцієнтом місцевого опору zМ,і,n; kі вертикальних ділянок kі = kі¢+ kі² (де kі¢ – з підйомним рухом середовища, kі² – з опускним рухом середовища). Прийнято, що на і-й ділянці може спостерігатися: на частині ділянки l i¢ – рух однофазного середовища, на частині l i² – рух двофазного середовища, причому Li = l i¢ + l i². Математичний опис теплогідродинамічних процесів у дренажному каналі складається із таких основних рівнянь: - конфігурація і опір ДКСК
за умов:
переріз з координатою l:
для однофазного потоку
для двофазного потоку
- рівняння суцільності
- перепад тиску між початковим перерізом і перерізом закипання
- перепад тиску в ДК
- рівняння балансу енергії для двофазного потоку
|

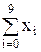 = 550,
= 550,  = 38500,
= 38500, 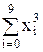 = 3,025×106,
= 3,025×106,  = 2,533×108,
= 2,533×108, 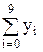 = 297,4,
= 297,4,  = 24705,
= 24705,  = 2,156×106.
= 2,156×106. .
.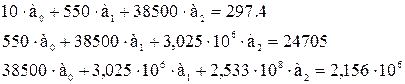 .
. ,
,  .
.
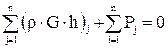 ; (8.1)
; (8.1) ; (8.2)
; (8.2) ; (8.3)
; (8.3)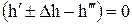 . (8.4)
. (8.4)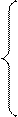
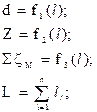
 ;
;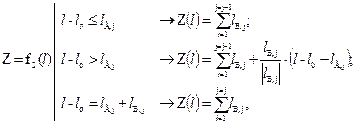
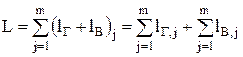 ;
; 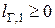 ;
;  ;
; 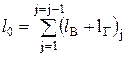 ;
;
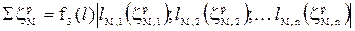 ;
; ;
; ;
; ;
;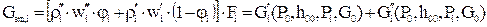 ;
;
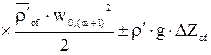 ;
; ;
;
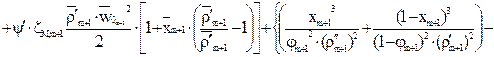
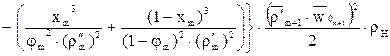 ;
;