Розв’язання. Процес нагрівання конвекцією термічно тонкого тіла описується рівнянням
Процес нагрівання конвекцією термічно тонкого тіла описується рівнянням
де V та F – об’єм та площа поверхні нагріву тіла, T – температура тіла. Виконуючи нескладні арифметичні дії наведене вище рівняння можна перетворити на наступне
Розв’яжемо дане рівняння методом Ейлера. Оберемо крок h = 50 с. Час нагрівання позначимо – х, а температуру металу – y. Тоді за залежністю (4.2) для часу t = 50 с значення температури
Аналогічно виконаємо розрахунки для інших моментів часу. Отримаємо y100 = 370,75°С, y150 = 407,212°С, y200 = 444,352°С, y250 = 482,134°С, y300 = 520,528°С. Виконаємо розрахунки зміни температури металевої заготовки методом Рунге-Кутта четвертого порядку. Скористаємось залежностями (4.6) і визначимо функції k1, k2, k3 та k4 для моменту часу t = 50
Згідно із (4.5) температура заготовки у момент часу t = 0 + h = 50 с
Результати розрахунків для інших моментів часу зводимо у таблицю 4.1.
Таблиця 4.1 – Результати розрахунків за методом Рунге-Кутта
Задачі для самостійної роботи Приклад 4.2. Розв’язати завдання за прикладом 4.1 методом Ейлера та методом Рунге-Кутта 4 порядку в діапазоні, якщо …
5 НАБЛИЖЕННЯ ФУНКЦІЙ, АПРОКСИМАЦІЯ, ІНТЕРПОЛЯЦІЯ. МЕТОД НАЙМЕНШИХ КВАДРАТІВ
5.1 Постановка задачі
В цій лекції розглядаються найважливіші і найбільш поширені методи наближення – апроксимації – функцій однієї змінної. Обчислення значення функції у = f(х) – одна з тих задач, з якими постійно на практиці доводиться стикатися. Природно, що при вирішенні на ЕОМ серйозних задач бажано мати швидкі і надійні алгоритми обчислення значень функцій, що використовуються. Найбільш поширені випадки. 1. Функція f(х) задана таблицею своїх значень, а обчислення проводяться в точках х, що не співпадають з табличними. 2. Безпосереднє обчислення значення у = f(х) зв’язано з проведенням складних розрахунків і приводить до значних витрат машинного часу, які можуть виявитися неприйнятними, якщо функція f(х) обчислюється багато разів. 3. При заданому значенні х значення f(х) може бути знайдене з експерименту. Проблеми, що виникають, нерідко вдається вирішити завдяки використанню інтерполяції – заміни f(x) іншою приблизною функцією g(х), обчислювані значення якої і приймають за наближені значення функції f(х). Така заміна виправдана лише тоді, коли значення g(х) обчислюються швидко і надійно, а погрішність наближення f(х) - g(х) достатньо мала. Однією з найскладніших задач є правильний вибір класу наближувальної функції g(х). Якщо необхідно отримати наближення функції f(х) для значення х, яке не належить дослідженому відрізку, (виконати прогноз поводження функції) то такий метод наближення називають екстраполяцією.
5.2 Поліноміальная інтерполяція Почнемо з розгляду задачі інтерполяції в найпростішому і повно дослідженому випадку інтерполювання многочленами алгебри. З використанням інтерполяційного багаточлена можна записати систему
Ця система однозначно вирішувана, і має єдиний розв’язок. На практиці система (5.1) ніколи не використовується для обчислення коефіцієнтів інтерполяційного багаточлена. Річ у тому, що часто вона є погано обумовленою. Крім того, існують різні зручні явні форми запису інтерполяційного багаточлена, які і застосовуються при інтерполяції. Многочлен Лагранжа. Приведемо одну з форм запису інтерполяційного багаточлена – багаточлен Лагранжа
де
В інженерній практиці найчастіше використовують інтерполяцію багаточленами першої, другої та третьої степені (лінійна, квадратична, кубічна). Тоді для інтерполяції першої та другої степені
Поліноміальна інтерполяція однією апроксимаційною функцією має недолік – велика кількість розрахунків, чутливість до вхідних даних та ін. Тому на практиці використовують кусково-поліноміальну інтерполяцію, інтерполяцію із рухомим поліномом, інтерполяцію сплайнами тощо.
5.3 Метод найменших квадратів Задача найменших квадратів виникає в самих різних областях науки і техніки. Наприклад, до неї приходять при статистичній обробці експериментальних даних за допомогою регресійного аналізу. В інженерній діяльності задача найменших квадратів використовується в таких областях, як оцінювання параметрів і фільтрація. 1. Лінійна задача найменших квадратів.
Якщо значення у, отримані з експерименту, то помилки носять випадковий характер і часто рівень погрішності ("шуму" таблиці) буває значним (рис. 5.1, а). Припустімо, що для апроксимації функції використовується лінійна модель. У разі, коли рівень невизначеності початкових даних високий, неприродно вимагати від моделі виконання умов збігу значень апроксимаційної функції із заданими значеннями y, тобто використовувати інтерполяцію. Але при інтерполяції (див. рис. 5.1, б) відбувається повторення помилок спостережень, тоді як при обробці експериментальних даних бажано, навпаки, їх згладжування. З різних критеріїв, що дозволяють вибрати параметри апроксимаційної функції Ф(х), найбільш часто використовується критерій найменших квадратів. Згідно цього критерію параметри вибираються так, щоб мінімізувати середньоквадратичне відхилення
Дуже часто для наближення за методом найменших квадратів використовуються багаточлени алгебри. У разі, коли наближення здійснюється багаточленом першого ступеня Ф(х)= а0 + а1×х, система має вигляд
Для багаточлена другого ступеня Ф(х)= а0 + а1×х + а2×х2 система має вигляд
Контрольні запитання
1. Наведіть приклади необхідності використання методів наближення функцій. 2. Поясніть відмінність інтерполяції та екстраполяції функцій. 3. Поясніть метод поліноміальної інтерполяції. 4. Поясніть використання багаточлена Лагранжа першого та другого степеню для інтерполяції функцій. Поясніть недоліки такого метода. 5. Поясніть метод найменших квадратів апроксимації функцій.
|

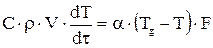 ,
,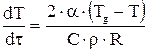 .
. °С.
°С.
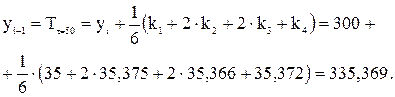
 . (5.1)
. (5.1) , (5.2)
, (5.2) .
. , (5.3)
, (5.3)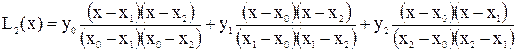 . (5.4)
. (5.4)
 . (5.5)
. (5.5) . (5.6)
. (5.6)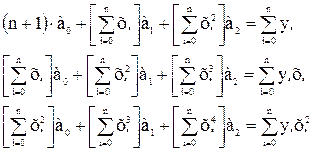 . (5.7)
. (5.7)


