Приклади оформлення результатів числових досліджень
Таблиця 8.1 – Доцільність використання конденсаційного теплообмінника в водогрійному котлі малої потужності
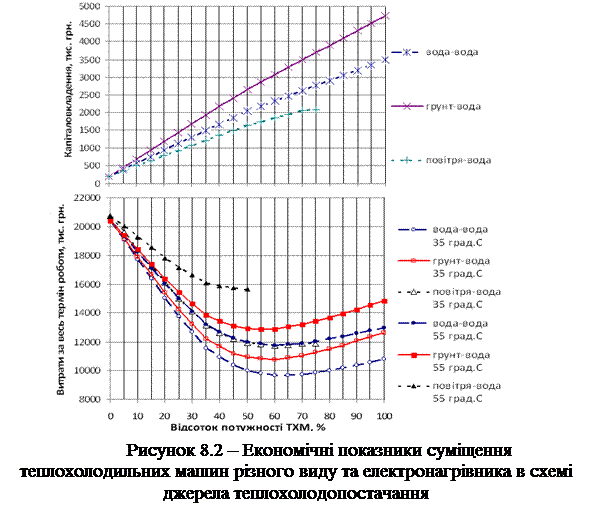
Згідно результатів, наведених в табл. 8.1, можна зробити висновок, що найкращі економічні показники має варіант водогрійного котла із водяним конденсаційним теплообмінником. Аналіз результатів, наведених на рис. 8.2, дозволяє зробити висновок про оптимальну частку потужності теплохолодильної машини в складі системи, що забезпечує мінімум грошових витрат протягом терміну роботи обладнання.
Контрольні запитання 1. Охарактеризуйте основні етапи створення моделі теплоенергетичного об’єкту з врахуванням системного підходу. 2. Наведіть приклади впливу зовнішніх зв’язків системи на її основні характеристики та показники. 3. Охарактеризуйте основні рівняння математичного опису теплоенергетичного об’єкту. 4. Поясніть обмеження та спрощення, які можуть використовуватись при побудові математичних моделей теплоенергетичних об’єктів. 5. Наведіть основні складові загальної характеристики математичної моделі. 6. Поясніть як слід висвітлювати характеристику математичного опису моделі. 7. Поясніть яким чином слід представляти отримані результати числових досліджень. Завдання для самостійної роботи Приклад 8.1. Скласти математичний опис для моделі, що розробляється в рамках дипломного проектування. Навести загальну характеристику розроблюваної математичної моделі. 9 ОПТИМІЗАЦІЯ В ТЕПЛОЕНЕРГЕТИЧНИХ ЗАДАЧАХ
9.1 Критерії оптимізації теплоенергетичних об’єктів
Критерієм оптимізації об’єкту є показник, екстремум якого (максимум або мінімум) відповідає найвищому рівню оптимальності об’єкта. Виділяють часткові та узагальнені критерії оптимізації. Існують також багатокритеріальні методи оптимізації. Часткові критерії не дозволяють в повній мірі оцінити оптимальність варіанту. Наприклад, частковим критерієм оптимізації теплообмінника можна назвати компактність або питому масу. Як бачимо ці показники не характеризують інші важливі особливості теплообмінника, як вартість, складність технології виготовлення тощо. Існують розробки (в тому числі, з використанням нечіткої логіки), коли узагальнений критерії представляють як суму часткових критеріїв, помножених на коефіцієнт ваги критерія. Найскладнішим в цим методах є визначити вагу кожного критерія, тому для цього переважно використовують експертну інформацію. Одним з найуживаніших узагальнених критеріїв оптимізації на даний момент є мінімум приведених витрат. Цей показник економічного метода виражається в грошових одиницях. Інший вигляд такого показника – термін окупності капіталовкладень. Такий критерій оптимізації використовується для вирішення задач в різних галузях економіки. В задачах теплоенергетики до останнього часу він був достатньо ефективним, але на сучасному етапі розвитку суспільства, при теперішньому стані навколишнього середовища він має суттєвий недолік – недостатнє врахування впливу об’єкта на навколишнє середовище. Використання методів оцінки життєвого циклу в екологічних показниках, наприклад, методу Есо-indicator, дозволяє перевести різні витрати, в тому числі, енергетичні і матеріальні, на протязі життєвого циклу, починаючи з видобування корисних копалин для створення об’єкту, закінчуючи етапом його утилізації, в єдині показники – Pt (ecopoint). Варіант з мінімальним техногенним навантаженням на навколишнє середовище є оптимальним.
9.2 Методи пошуку екстремуму
Існує багато метод пошуку екстремума (мінімума або максимума) функції в певному діапазоні значень.
Метод пасивного пошуку екстремуму Метод вирішення поставленого завдання, в якому задається правило обчислення або відомі значення функції відразу для всіх точок x1, x2, …, xn, називається методом пасивного пошуку. За xextr приймається така точка xi для якої f(xi) = min(f(xi)) або f(xi) = max(f(xi)). Цей метод полягає у почерговому перебиранні аргументів і використанні нерівностей
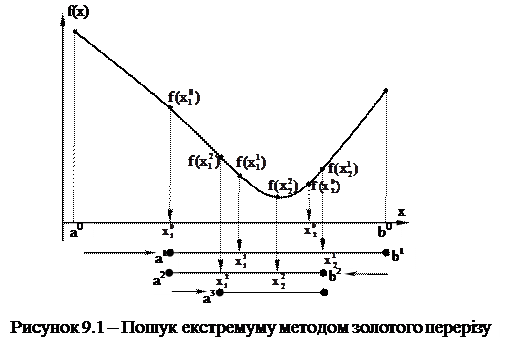
Метод золотого перерізу Реалізація цього методу для пошуку екстремуму заснована на використанні принципу послідовного скорочення відрізка локалізації. При цьому враховується таке припущення: якщо функція унімодальна на відрізку [a,b], то вона унімодальна на будь-якому відрізку [c,d] Î [a,b]. Кожна наступне наближення можна зробити, обчисливши додатково значення функції лише в одній новій точці. Золотим перерізом відрізка називається таке розбиття відрізка на дві нерівні частини, при якому відношення довжини всього відрізка до довжини його великої частини дорівнює відношенню довжини більшої частини до довжини меншої частини відрізка. Співвідношення, за допомогою яких визначаються значення точок розбиття відрізка відповідно до правила золотого перетину: x1 = 0,618×a + 0,382×b, x2 = 0,382×a + 0,618×b. Потім проводять обчислення значень функції в точках знайдених f(x1) і f(x2). Якщо f(x1) < f(x2), то вибирають для подальшого поділу відрізок [a, x2], якщо ж f(x1) > f(x2), то вибирають [x1, b]. У першому випадку однією з двох поділяють точок вибраного відрізка буде x1, y другому x2. Це випливає з властивостей золотого перерізу (рис. 9.1).
Ітеративні наближення продовжують здійснювати до тих пір, поки Метод покоординатного спуску і градієнтний метод Більшість ітераційних методів, що застосовуються для вирішення задачі безумовної оптимізації функції багатьох змінних, відносяться до класу методів спуску, тобто таких методів, для яких кожна ітерація (крок) призводить до зменшення значення цільової функції: f(xi+1) < f(xi), для всіх i, що не дорівнюють 0. Кожен наступний крок виглядає так. 1. Знаходять нульовий вектор pi – напрям спуску. Цей вектор повинен бути таким, щоб при всіх досить малих кроках спуску ai виконувалося нерівність: f(xi + ai×pi) < f(xi). 2. Обчислюють позитивне число ai (крок спуску), для якого виконується вищенаведене нерівність. 3. За чергове наближення до точки мінімуму беруть xi+1=xi + ai×pi. 4. Перевіряють виконання критерію ітерацій. Якщо зміна параметрів менше заданої похибки, то ітерації припиняють і вважають xextr = xi+1. В іншому випадку ітерації продовжують далі.
У методі покоординатного спуску в якості чергового напрямку спуску обирають напрямок однієї з координатних осей (рис. 9.2).
Найбільш відомим є метод циклічного покоордінатного узвозу. Алгоритм координатного спуску полягає у зведенні багатовимірної задачі до послідовних одновимірних завдань, які у свою чергу вирішуються методами мінімізації функції однієї змінної, наприклад, методом золотого перерізу. Градієнтний метод відрізняється тим, що спочатку визначається напрям найшвидшого зменшення функції – градієнт рі. З початкової точки продовжується спуск вздовж градієнта до тих пір, поки не буде знайдене найменше значення функції. Далі будується перпендикулярний градієнт і відбувається наступний спуск.
Метод випадкового пошуку Цей метод полягає в наступному. Спочатку вибирають довільну точку з області аргументів (
Якщо такої точки не знаходиться, то звужують радіус області для уточнення координат мінімуму. Метод не бездоганний, оскільки вимагає великого об’єму обчислень, що збільшує час рахунку.
Контрольні запитання 1. Дайте визначення та класифікацію методів оптимізації. 2. Охарактеризуйте часткові критерії оптимізації об’єктів, наведіть приклади. 3. Охарактеризуйте відомі узагальнені критерії оптимізації. 4. Поясніть метод пасивного пошуку оптимуму. 5. Поясніть метод золотого перерізу оптимізації об’єктів. 6. Поясніть відмінність метода покоординатного спуску та градієнтного метода пошуку оптимуму.
Завдання для самостійної роботи Приклад 9.1. Розробити оптимізаційну модель теплообмінника, вибрати метод та критерій оптимізації, провести дослідження з пошуку екстремуму при зміні швидкості теплоносія та при зміні поперечного перерізу каналів. Приклад 9.2. Розробити оптимізаційну модель теплової мережі, вибрати метод та критерій оптимізації, провести дослідження з пошуку екстремуму при зміні швидкості теплоносія та при зміні товщини теплоізоляції теплопроводу.
10 КЛАСИФІКАЦІЯ ТА ДЖЕРЕЛА ПОХИБОК. ПОХИБКИ РОЗРАХУНКОВИХ ВЕЛИЧИН
10.1 Класифікація похибок за джерелами виникнення
Важливо вміти оцінити точність розв'язку задачі, який здебільшого ми дістаємо з похибками. Похибки результатів зумовлюються такими причинами. 1. Математична модель лише наближено відображає реальні явища. 2. Вхідні дані, як правило, – це числа неточні (дані для обчислень часто дістають з експерименту, а кожний експеримент може дати результат лише з обмеженою точністю). 3. Метод розв'язування задачі часто є наближеним. У багатьох задачах точний результат можна дістати лише після нескінченної або досить великої кількості арифметичних операцій, які практично здійснити неможливо. Тому замість точного розв'язку здебільшого доводиться відшукувати наближений (наприклад, замість суми ряду беруть суму скінченої кількості його членів, нескінченний ітераційний процес обривають після скінченого числа ітерацій, інтеграл замінюють скінченою сумою і т. п.). 4. Округлення при обчисленнях. Усі обчислення (вручну і на ЕОМ) можна виконувати лише з обмеженою кількістю значущих цифр. Тому при виконанні арифметичних дій потрібно вдаватися до округлень, які зумовлюють похибки, що нагромаджуються в процесі обчислень. Похибки, що породжуються вищезгаданими причинами, відповідно називаються: 1) похибка математичної моделі; 2) неусувна похибка (вона не залежить від обчислювача); 3) похибка методу; 4) похибка округлень. Повна похибка результату дорівнює сумі всіх перерахованих похибок. Зауважимо, що похибок, пов'язаних з особливостями будови математичної моделі, не розглядатимемо. Похибки методів досліджуються для кожному окремого метода. На сучасних ЕОМ числа записуються також з достатньою кількістю значущих цифр, тому похибкою окремого округлення здебільшого можна нехтувати на противагу похибці методу і неусувній похибці. У процесі виконання великої кількості операцій похибка округлень збільшується. До значного нагромадження таких похибок може призвести віднімання близьких за величиною чисел, знаходження коренів многочленів високих степенів тощо.
10.2 Похибки наближених чисел
Часто на практиці з тих чи інших причин доводиться замість точного числа брати його наближене значення а. При цьому виникає похибка
Абсолютною похибкою
Граничною абсолютною похибкою вважають будь-яке число
Це означає, що Надалі ці нерівності скорочено записуватимемо Зауважимо, що найчастіше точне значення Абсолютна похибка не завжди характеризує точність. В таких випадках використовують відносну похибку наближеного числа а
Гранична відносна похибка визначається
Додатне число а можна записати у вигляді скінченого десяткового ряду K-та цифра наближеного числа а називається правильною, якщо абсолютна похибка
В іншому випадку цифру k-го розряду називають сумнівною. Значущими цифрами наближеного числа а називатимемо всі його правильні цифри, починаючи з першої зліва, що не дорівнює нулю (її десятковий розряд позначується m), до першої сумнівної цифри включно. Усі інші цифри називатимемо незначущими. Записуючи остаточні результати наближених обчислень, незначущі цифри числа відкидатимемо. Якщо з наближеними числами виконуватимуться обчислення, то в них, крім значущих, треба зберігати ще одну або дві сумнівні цифри. Якщо додатне наближене число а має n правильних значущих цифр, то його відносна похибка d задовольняє співвідношення
10.3 Похибки розрахункових величин
Нехай потрібно обчислити значення функції
Припустивши, що функція
плюс члени другого і вищих порядків відносно Dxi. Якщо похибки Dxi за абсолютною величиною досить малі, то членами другого і вищих порядків у виразі (10.9) можна знехтувати. Тоді для абсолютної похибки наближеного значення матимемо
Для граничної відносної похибки δy маємо
З формули (10.11) випливає, що гранична абсолютна похибка суми наближених чисел a1 + a2 +…+ an… дорівнює сумі їх граничних абсолютних похибок. Для різниці двох чисел a = a1 – a2 маємо: При цьому відносна похибка різниці Для похибки добутку додатних чисел а = а1 × а2... аn з (10.11) маємо
тобто гранична відносна похибка добутку кількох наближених додатних чисел, що відрізняються від нуля, дорівнює сумі граничних відносних похибок цих чисел. Легко переконатись, що гранична відносна похибка частки дорівнює сумі граничних відносних похибок діленого і дільника. Можна переконатися також, що відносна похибка k-то степеня числа а у k раз більша, ніж відносна похибка числа а. Аналогічно, відносна похибка кореня k-гo порядку з числа a у k раз менша, ніж відносна похибка числа а.
10.4 Поняття про імовірну оцінку похибки
Наближене число а може відхилятися від точного числа Розглянемо суму наближених чисел a = a1 + a2 +…+ an. Гранична абсолютна похибка суми Вважатимемо, що випадкові величини Таким чином, абсолютна похибка суми наближених чисел a = a1 + a2 +…+ an пропорційна числу Аналогічно приходимо до висновку, що й відносна похибка добутку наближених чисел a1, a2, …, an зростає пропорційно числу
10.5 Обчислення без точного врахування похибок
Точний підрахунок похибок результатів обчислень наближених чисел досить громіздкий. Тому здебільшого на практиці точно не враховують похибок, а користуються правилами підрахунку цифр за В. М. Брадісом. 1. При додаванні і відніманні наближених чисел молодший збережений розряд результату має бути найбільшим серед розрядів, що виражаються останніми значущими цифрами вихідних даних. 2. При множенні і діленні наближених чисел у результаті потрібно зберегти стільки значущих цифр, скільки їх має наближене дане з найменшою кількістю значущих цифр. 3. При піднесенні до квадрата або до куба в результаті треба зберегти стільки значущих цифр, скільки їх має число, яке підносять до степеня. 4. При добуванні кореня в результаті слід брати стільки значущих цифр, скільки їх у підкореневому виразі. 5. При обчисленні проміжних результатів потрібно брати на одну-дві цифри більше, ніж рекомендують попередні правила. 6. Якщо дані можна брати з довільною точністю, то, щоб знайти результат з k правильними цифрами, дані треба брати з такою кількістю цифр, яка забезпечує 7. При обчисленнях одночленних виразів за допомогою логарифмів слід підрахувати кількість значущих цифр у тому наближеному даному, у якому їх найменше, і взяти таблицю логарифмів з кількістю знаків на одиницю більшою. У кінцевому результаті остання цифра відкидається. Зауважимо, що в основу цих правил покладено принцип академіка О.М. Крилова – основний принцип звичайних обчислень, тобто обчислень без строгого врахування похибок: наближене число слід писати так, щоб у ньому всі цифри, крім останньої, були правильними і лише остання була сумнівною, притому не більш як на одну одиницю.
Контрольні запитання 1. Поясніть причини виникнення похибок. 2. Охарактеризуйте різновиди похибок. 3. Поясніть відмінність між абсолютною похибкою та граничною абсолютною похибкою. 4. Поясніть, як визначається чи правильною є цифра наближеного числа. 5. Які цифри наближеного числа є значущими і які – незначущими. 6. Поясніть як розраховуються абсолютні похибки суми та різниці наближених чисел. 7. Поясніть як розраховуються відносні похибки суми та різниці наближених чисел. 8. Поясніть як розраховуються відносні похибки добутку, ділення, піднесення до степеню та добування кореню наближених чисел. 9. Поясніть, особливості визначення імовірних похибок розрахункових величин. 10. Наведіть правила обчислення величин без точного врахування похибок.
|

 або
або 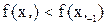 . Тоді xextr буде належати діапазону [хі-1; хі+1]. Похибка визначення екстремуму дорівнюватиме
. Тоді xextr буде належати діапазону [хі-1; хі+1]. Похибка визначення екстремуму дорівнюватиме 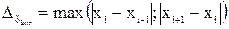 .
.
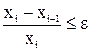 , де e - похибка обчислень (задана точність).
, де e - похибка обчислень (задана точність).
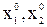 ) i в ній обчислюють значення функції у0.
) i в ній обчислюють значення функції у0.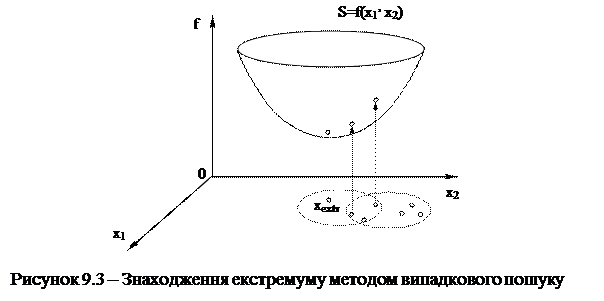
 . (10.1)
. (10.1)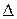 наближеного числа а називають величину
наближеного числа а називають величину . (10.2)
. (10.2)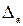 , що задовольняє умову
, що задовольняє умову . (10.3)
. (10.3)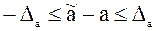 .
.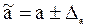 .
.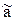 буває невідомим, а тому невідома й похибка D наближеного числа а.
буває невідомим, а тому невідома й похибка D наближеного числа а.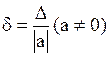 . (10.4)
. (10.4)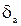
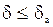 . (10.5)
. (10.5)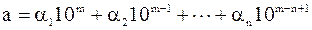 .
.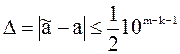 . (10.6)
. (10.6)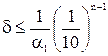 . (10.7)
. (10.7)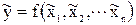 при заданих значеннях незалежних змінних. Якщо при цьому замість точних значень
при заданих значеннях незалежних змінних. Якщо при цьому замість точних значень  , які нам не відомі, підставляються їх наближені значення
, які нам не відомі, підставляються їх наближені значення 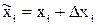 ,
, 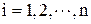 ), то при обчисленні значення функції виникає похибка
), то при обчисленні значення функції виникає похибка . (10.8)
. (10.8)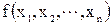 диференційована (достатню кількість разів), Dy можна подати у вигляді
диференційована (достатню кількість разів), Dy можна подати у вигляді (10.9)
(10.9)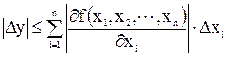 . (10.10)
. (10.10) або
або 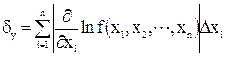 . (10.11)
. (10.11) .
.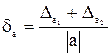 може виявитись досить великою, якщо числа а1 та а2 між собою мало відрізняються і їх різниця близька до нуля. У цьому випадку для забезпечення потрібної точності треба мати в зменшуваному і від’ємнику достатню кількість цифр, щоб гранична абсолютна похибка різниці а була меншою від самої різниці. Тому, по можливості, слід уникати віднімання близьких чисел.
може виявитись досить великою, якщо числа а1 та а2 між собою мало відрізняються і їх різниця близька до нуля. У цьому випадку для забезпечення потрібної точності треба мати в зменшуваному і від’ємнику достатню кількість цифр, щоб гранична абсолютна похибка різниці а була меншою від самої різниці. Тому, по можливості, слід уникати віднімання близьких чисел.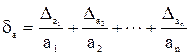 , (10.12)
, (10.12)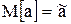 . Сама похибка
. Сама похибка 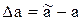 також є випадковою величиною з математичним сподіванням, що дорівнює нулю,
також є випадковою величиною з математичним сподіванням, що дорівнює нулю, 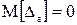 .
. .
. мають один і той самий нормальний розподіл ймовірностей з математичним сподіванням, що дорівнює нулю, і середнім квадратичним відхиленням s. Тоді, як відомо з курсу теорії ймовірностей, математичне сподівання суми випадкових величин дорівнює сумі їх математичних сподівань. Дисперсія суми незалежних випадкових величин дорівнює сумі дисперсій цих величин, тобто
мають один і той самий нормальний розподіл ймовірностей з математичним сподіванням, що дорівнює нулю, і середнім квадратичним відхиленням s. Тоді, як відомо з курсу теорії ймовірностей, математичне сподівання суми випадкових величин дорівнює сумі їх математичних сподівань. Дисперсія суми незалежних випадкових величин дорівнює сумі дисперсій цих величин, тобто  (нагадаємо, що за означенням середнє квадратичне відхилення
(нагадаємо, що за означенням середнє квадратичне відхилення  випадкової величини X дорівнює
випадкової величини X дорівнює 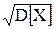 , де
, де 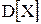 – дисперсія випадкової величини X, а тому
– дисперсія випадкової величини X, а тому  .
.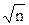 , а не числу n, як це випливало з формули (10.10). Це пояснюється тим, що практично похибки різних чисел можуть частково «гасити» одна одну, в той час як формула (10.10) передбачає, так би мовити, крайній випадок.
, а не числу n, як це випливало з формули (10.10). Це пояснюється тим, що практично похибки різних чисел можуть частково «гасити» одна одну, в той час як формула (10.10) передбачає, так би мовити, крайній випадок. правильну цифру в результаті відповідно до правил 1-4.
правильну цифру в результаті відповідно до правил 1-4.


