Определение активного давления на вертикальную гладкую стенку при горизонтальной поверхности засыпки.
Рассмотрим простейший случай, когда засыпка представлена идеально сыпучим грунтом (рис. 6.8). Поскольку принято, что стенка имеет абсолютно гладкую грань, т. е. трение грунта о стенку отсутствует (
где В пределах призмы обрушения ОАВ грунт находится в состоянии предельного равновесия. Следовательно, минимальное главное напряжение в этой точке
Тогда с учетом формулы (6.12) активное давление грунта на стенку в точке, расположенной на глубине z от поверхности засыпки, будет равно
Форма уравнения (6.14) показывает, что в рассматриваемом случае эпюра активного давления имеет вид треугольника. Подставив в это уравнение высоту стенки
Равнодействующая активного давления
и будет приложена к стенке на расстоянии Из анализа равновесия призмы обрушения несложно установить, что плоскость скольжения АВ будет наклонена к вертикали под углом
|
), вертикальные и горизонтальные площадки являются главными. Тогда максимальное главное напряжение, действующее на горизонтальную площадку в точке контакта грунта со стенкой на глубине z от поверхности засыпки, будет равно
, (6.12)
– удельный вес грунта.
, равное активному давлению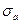 
, будет связано с максимальным главным напряжением условием предельного равновесия.
Условие предельного равновесия для сыпучих грунтов 
можно выразить в виде
. (6.13)
. (6.14)
, получим максимальную ординату эпюры активного давления:
. (6.15)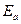
определится как площадь эпюры 
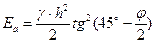, (6.16)
от ее подошвы.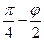
. Отсюда можно определить ширину призмы обрушения по поверхности засыпки 
.
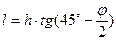