Этот случай является общим. Рассмотрим предельное равновесие призмы обрушения ОАВ согласно расчетной схеме, представленной на рис. 6.9, а. Здесь  – угол наклона задней грани стенки к вертикали;
– угол наклона задней грани стенки к вертикали;  – угол наклона поверхности засыпки к горизонтали (знак плюс соответствует восходящей, минус – нисходящей засыпке);
– угол наклона поверхности засыпки к горизонтали (знак плюс соответствует восходящей, минус – нисходящей засыпке); 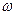 – угол отклонения равнодействующей
– угол отклонения равнодействующей 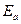 от нормали к стенке за счет трения грунта о стенку (для стенок с повышенной шероховатостью принимается равным
от нормали к стенке за счет трения грунта о стенку (для стенок с повышенной шероховатостью принимается равным 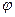 ; для мелкозернистых водонасыщенных песков и при вибрационных нагрузках
; для мелкозернистых водонасыщенных песков и при вибрационных нагрузках  , где
, где
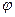 – расчетное значение угла внутреннего трения).
– расчетное значение угла внутреннего трения).
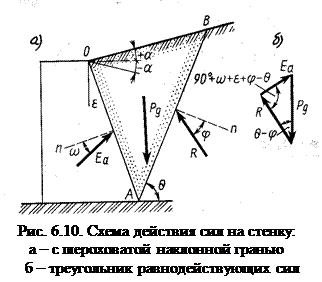 На призму обрушения ОАВ в предельном состоянии действуют следующие результирующие силы: собственный вес грунта
На призму обрушения ОАВ в предельном состоянии действуют следующие результирующие силы: собственный вес грунта 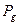 , реактивный отпор стенки
, реактивный отпор стенки 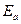 , реактивный отпор массива грунта
, реактивный отпор массива грунта  ниже поверхности скольжения АВ, отклоняющийся от нормали на угол
ниже поверхности скольжения АВ, отклоняющийся от нормали на угол 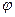 . Отметим, что значение угла наклона поверхности скольжения
. Отметим, что значение угла наклона поверхности скольжения  к горизонтали пока еще неизвестно и принимается произвольно. Определив из геометрических соображений величину
к горизонтали пока еще неизвестно и принимается произвольно. Определив из геометрических соображений величину 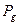 и, зная направление остальных усилий, можно, построив треугольник сил, определить величины
и, зная направление остальных усилий, можно, построив треугольник сил, определить величины 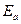 и
и  для принятого значения
для принятого значения  (рис. 6.10, б). Тогда
(рис. 6.10, б). Тогда
 . (6.25)
. (6.25)
Теперь необходимо найти такое значение угла  , при котором активное давление будет максимальным. Используя правило экстремума
, при котором активное давление будет максимальным. Используя правило экстремума 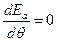 , окончательно получим
, окончательно получим
 , (6.26)
, (6.26)
где 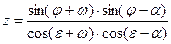 .
.
Формула (6.26) неприменима при крутых откосах (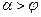 ), которые сами по себе неустойчивы, и для стенок с очень пологой задней гранью (при
), которые сами по себе неустойчивы, и для стенок с очень пологой задней гранью (при 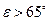 ).
).
В более сложных случаях применяются и другие методы, в частности графический метод К. Кульмана, позволяющий решать задачу при непроизвольном очертании поверхности грунта и любых схемах загружения. Этот метод подробно рассмотрен в литературе, например, в учебниках Б. И. Далматова и П. Л. Иванова.

 – угол наклона задней грани стенки к вертикали;
– угол наклона задней грани стенки к вертикали;  – угол наклона поверхности засыпки к горизонтали (знак плюс соответствует восходящей, минус – нисходящей засыпке);
– угол наклона поверхности засыпки к горизонтали (знак плюс соответствует восходящей, минус – нисходящей засыпке); 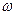 – угол отклонения равнодействующей
– угол отклонения равнодействующей 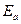 от нормали к стенке за счет трения грунта о стенку (для стенок с повышенной шероховатостью принимается равным
от нормали к стенке за счет трения грунта о стенку (для стенок с повышенной шероховатостью принимается равным 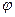 ; для мелкозернистых водонасыщенных песков и при вибрационных нагрузках
; для мелкозернистых водонасыщенных песков и при вибрационных нагрузках  , где
, где  На призму обрушения ОАВ в предельном состоянии действуют следующие результирующие силы: собственный вес грунта
На призму обрушения ОАВ в предельном состоянии действуют следующие результирующие силы: собственный вес грунта 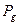 , реактивный отпор стенки
, реактивный отпор стенки  ниже поверхности скольжения АВ, отклоняющийся от нормали на угол
ниже поверхности скольжения АВ, отклоняющийся от нормали на угол  к горизонтали пока еще неизвестно и принимается произвольно. Определив из геометрических соображений величину
к горизонтали пока еще неизвестно и принимается произвольно. Определив из геометрических соображений величину  . (6.25)
. (6.25)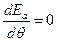 , окончательно получим
, окончательно получим , (6.26)
, (6.26)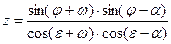 .
.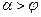 ), которые сами по себе неустойчивы, и для стенок с очень пологой задней гранью (при
), которые сами по себе неустойчивы, и для стенок с очень пологой задней гранью (при 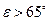 ).
).


