При наличии на поверхности сплошной равномерно распределенной нагрузки интенсивностью  (рис. 6.9, а) выражение (6.12) будет иметь вид
(рис. 6.9, а) выражение (6.12) будет иметь вид
 . (6.17)
. (6.17)
Повторяя те же рассуждения, получим
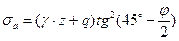 , (6.18)
, (6.18)
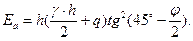 (6.19)
(6.19)
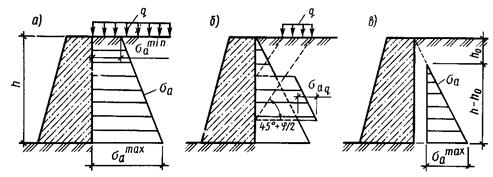
Рис. 6.9. Схемы для определения активного давления:
а – при равномерно распределенной нагрузке; б – при местной нагрузке; в – для случая засыпки связным грунтом
Из приведенных выражений можно получить значения 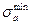 при
при 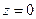 и
и  при
при  и убедиться, что эпюра активного давления имеет вид трапеции. Точка приложения равнодействующей
и убедиться, что эпюра активного давления имеет вид трапеции. Точка приложения равнодействующей 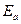 будет находиться в центре тяжести площади трапеции, и расстояние от подошвы стенки до направления действия этой силы составит
будет находиться в центре тяжести площади трапеции, и расстояние от подошвы стенки до направления действия этой силы составит  .
.
Если на поверхности засыпки в пределах призмы обрушения приложена местная полосовая нагрузка  шириной
шириной 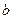 , то для определения дополнительного влияния этой нагрузки на величину активного давления используется следующий прием (рис. 6.9, б). Считают, что воздействие нагрузки на стенку передается под углом к горизонтали
, то для определения дополнительного влияния этой нагрузки на величину активного давления используется следующий прием (рис. 6.9, б). Считают, что воздействие нагрузки на стенку передается под углом к горизонтали  , а дополнительное активное давление от нее составляет
, а дополнительное активное давление от нее составляет
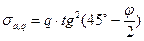 . (6.20)
. (6.20)
Эпюра активного давления для этого случая показана на рис. 6.9, б. Равнодействующая активного давления 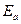 находится как площадь полной эпюры, а точка ее приложения соответствует центру тяжести эпюры активного давления.
находится как площадь полной эпюры, а точка ее приложения соответствует центру тяжести эпюры активного давления.
Учет сцепления грунта. Для связного грунта, обладающего внутренним трением и сцеплением, условие предельного равновесия  может быть представлено в виде
может быть представлено в виде
 (6.21)
(6.21)
Тогда значение ординаты активного давления связного грунта на глубине z можно получить в виде
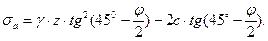 (6.22)
(6.22)
Известно, что связный грунт обладает способностью держать вертикальный откос высотой 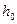 , определяемой по формуле
, определяемой по формуле  . Она может быть преобразована к виду
. Она может быть преобразована к виду
 . (6.23)
. (6.23)
Отсюда следует, что в пределах глубины 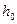 от свободной поверхности засыпки связный грунт не будет оказывать давления на стенку. Максимальная ордината эпюры активного давления связного грунта в соответствии с (6.22) определится как
от свободной поверхности засыпки связный грунт не будет оказывать давления на стенку. Максимальная ордината эпюры активного давления связного грунта в соответствии с (6.22) определится как
 (6.24)
(6.24)
Характер эпюры активного давления приведен на рис. 6.9, в. Можно заметить, что учет сцепления грунта приводит к уменьшению активного давления. Значение результирующей силы 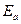 определяется как площадь треугольной эпюры
определяется как площадь треугольной эпюры 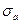 , имеющей высоту
, имеющей высоту 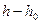 и максимальную ординату
и максимальную ординату 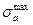 .
.

 (рис. 6.9, а) выражение (6.12) будет иметь вид
(рис. 6.9, а) выражение (6.12) будет иметь вид . (6.17)
. (6.17)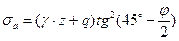 , (6.18)
, (6.18)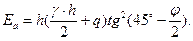 (6.19)
(6.19)
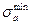 при
при 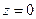 и
и  при
при  и убедиться, что эпюра активного давления имеет вид трапеции. Точка приложения равнодействующей
и убедиться, что эпюра активного давления имеет вид трапеции. Точка приложения равнодействующей 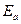 будет находиться в центре тяжести площади трапеции, и расстояние от подошвы стенки до направления действия этой силы составит
будет находиться в центре тяжести площади трапеции, и расстояние от подошвы стенки до направления действия этой силы составит  .
.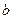 , то для определения дополнительного влияния этой нагрузки на величину активного давления используется следующий прием (рис. 6.9, б). Считают, что воздействие нагрузки на стенку передается под углом к горизонтали
, то для определения дополнительного влияния этой нагрузки на величину активного давления используется следующий прием (рис. 6.9, б). Считают, что воздействие нагрузки на стенку передается под углом к горизонтали  , а дополнительное активное давление от нее составляет
, а дополнительное активное давление от нее составляет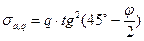 . (6.20)
. (6.20) может быть представлено в виде
может быть представлено в виде (6.21)
(6.21)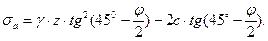 (6.22)
(6.22)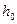 , определяемой по формуле
, определяемой по формуле  . Она может быть преобразована к виду
. Она может быть преобразована к виду . (6.23)
. (6.23) (6.24)
(6.24)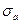 , имеющей высоту
, имеющей высоту 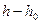 и максимальную ординату
и максимальную ординату 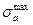 .
.


