Типові технологічні процеси та моделі об’єктів керування.
Математичне моделювання реалізується у трьох взаємопов’язаних стадіях: - формалізація процесу – побудова математичної моделі (складання математичного опису об’єкту чи системи); - програмування розв’язку задачі (розробка алгоритмів та програм) для знаходження числових значень параметрів; - встановлення відповідності (адекватності) математичної моделі. Побудова математичної моделі починається з формалізованого опису об’єкту моделювання. Аналітичний аспект моделювання складається із смислового описування об’єкта у математичній формі, у вигляді сукупності співвідношень між окремими параметрами моделі. Рівняння, які виражають залежність вихідних координат об’єкту від вхідних, називаються статичними характеристиками, які необхідно під час проектування технологічного процесу, визначення нормальних режимів роботи устаткування, оптимізації технологічних процесів і конструювання об’єктів із заздалегідь заданими властивостями. Для стаціонарних об’єктів сталий режим є незмінним у часі і не залежить від часу. Рівняння статистики можуть бути зображені як в алгебраїчній, так і в диференціальній формі. Для реактору з мішалкою для гомогенної реакції статична характеристика має вигляд:
де Для трубчатого реактора рівняння статики має вигляд:
де Сукупність математичних виразів, які описують зміну в часі вихідних координат об’єкту - це математичний опис його динаміки. Рівняння, які встановлюють залежність вихідних координат від зміни вхідних збурюючих параметрів, називаються динамічними характеристиками. Динамічні характеристики об’єктів, як правило, описуються диференціальними рівняннями. Залежність вихідних координат від часу при зміні вхідних називається перехідним процесом об’єкту або системи керування. Перехідні процеси в об’єктах із зосередженими параметрами описуються лінійними диференціальними рівняннями. Наприклад зміну концентрації y1(t) речовини в реакторі ідеального змішування можна описати рівнянням:
де V – об’єм реактора; F1,F2 – витрати речовини на його вході і виході; Wp – швидкість утворення продукту реакції; y1(t); y2(t) – відповідно, вхідна та вихідна концентрації. Динаміка об’єктів з розподіленими параметрами описуються диференціальним рівнянням з частинними похідними, які містять похідні за часом. Наприклад, для трубчастого реактору ідеального витіснення диференціальне рівняння має вигляд:
де l – координата по довжині труби; V – швидкість потоку. Статичні характеристики входять в рівняння динаміки об’єктів керування в явній чи неявній формі.
|

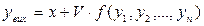 , (1.1)
, (1.1) , х – концентрація речовини на виході та вході апарату з об’ємом V; y 1, y 2… - концентрації речовини всередині апарату.
, х – концентрація речовини на виході та вході апарату з об’ємом V; y 1, y 2… - концентрації речовини всередині апарату.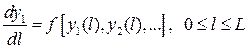 , (1.2)
, (1.2) - концентрації речовини y 1, y 2 – в перерізі, розміщеному на відстані l від входу в апарат; l – довжина апарату.
- концентрації речовини y 1, y 2 – в перерізі, розміщеному на відстані l від входу в апарат; l – довжина апарату.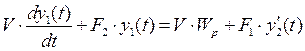 (1.3)
(1.3)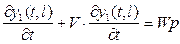 , (1.4)
, (1.4)


