Побудова ER-моделі за методом К.М.Бахмана
Вперше поняття ER- моделі запровадив Пітер Чен у 1976 році. Підхід П.Чена дозволив концептуальне моделювання перевести в практичну площину проектування БД. У подальшому діаграми П.Чена набули розвитку у багатьох інших роботах з ER-моделювання. До них належать такі моделі: · “пташина лапка”, розроблена К.М.Бахманом; · IDEF1X, розроблена Т.Ремеєм; · уніфікована мова моделювання UML; · модель Баркера і багато інших моделей. Модель “пташина лапка” (Crow’s Foot Model) розглядає сумісно інформацію про зв’язність і потужність зв’язку в єдиному наборі символів. Ця модель відображає лише три значення потужності 0, 1, N. Розглянемо ER- модель на основі символіки П.Чена і К.М.Бахмана.
Рис.4. Представлення сутностей і атрибутів:
Представлення зв’язків між відношеннями на діаграмі “пташина лапка” відображено на рис.5
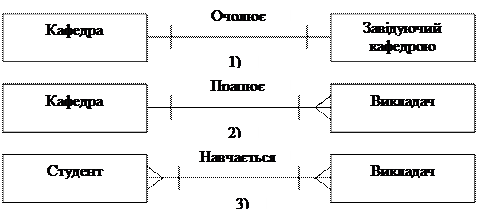
Рис.5.. Представлення зв’язків між відношеннями на діаграмі
На діаграмі ”пташина лапка” відображуються сильні і слабкі зв’язки. Якщо одна сутність незалежна від існування іншої сутності, то зв’язок між ними називається не ідентифікаційним зв’язком або слабким зв’язком. На ER- діаграмах ”пташина лапка” слабкий зв’язок відображується штриховою лінією (рис.6а). Ідентифікаційний зв’язок або сильний зв’язок має місце у тому випадку, коли одна зв’язана сутність залежить від існування іншої. На ER- діаграмах ”пташина лапка” сильний зв’язок відображується суцільною лінією (рис.6-б). Так сутність Студент не залежить від сутності Група, і тому зв’язок між сутностями відображується штриховою лінією. У той же час сутність Нагорода залежить від сутності Студент, в цьому випадку зв’язок між сутностями відображається суцільною лінією.
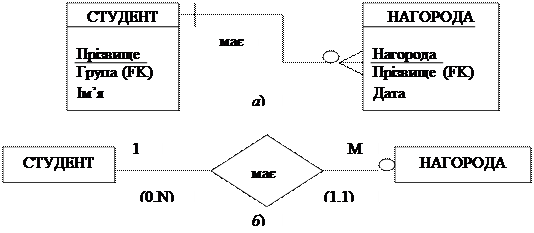
Рис.6. Не ідентифікаційний (а) та ідентифікаційний (б) зв’язки
Обов’язкові і необов’язкові зв’язки. Участь сутності у зв’язку може бути обов’язковою і необов’язковою. Необов’язковість зв’язку означає, що мінімальна кардинальність зв’язку має значення 0, яка на діаграмах позначається невеликим колом (рис.7.).
Рис.7. Необов’язкова сутність Нагорода в ER- діаграмах П.Чена і “пташина лапка”. Слабка сутність на діаграмі Чена позначається подвійним прямокутником, а на діаграмі “пташина лапка” – невеликими сегментами в кожному з кутів прямокутника (рис.8.).
Рис.8. Слабка сутність на діаграмах П. Чена і “пташина лапка”
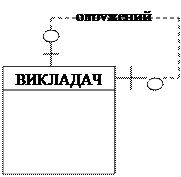
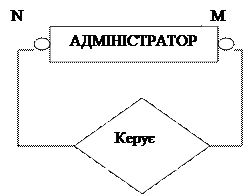
Рекурсивний зв’язок має місце, коли є зв’язок між екземплярами одного і того ж набору сутностей (рис.9.). Зв’язок 1:1 представляє висловлювання: “викладач може бути одружений тільки з одним співробітником”. Зв’язок M:N представляє висловлювання: “адміністратор має декілька підлеглих адміністраторів, і в свою чергу адміністратор має декілька керівників-адміністраторів”
Рис.9. Представлення рекурсивних зв’язків на діаграмі П.Чена і моделі “пташина лапка“
|