Метод определения модуля деформации грунта по результатам штамповых испытаний.
Штамповые испытания заключаются в том, что штамп - круглая плита - устанавливается на дно котлована на предварительно зачищенную и разровненную поверхность грунта, после чего загружается ступенями нагрузки. Последующая ступень нагрузки прикладывается после затухания осадки от предыдущей ступени. По линейному участку зависимости осадки
21. Метод определения модуля деформации грунта по результатам прессиометрических испытаний. Прессиометр представляет собой закрытый цилиндр с резиновой боковой поверхностью в который подается давление Р и измеряется увеличение диаметра цилиндра Dp (после стабилизации). По отношению Dp/Dd/ устанавливается по линейному участку диаграммы величина модуля деформацииE0. В обычных случаях для вычисления E0 нужно знать коэффициент Пуассона грунта. Мы получаем при этом испытании модуль деформации в горизонтальном, а не в вертикальном направлении, в то время как в грунтах, являющихся природными образованиями, деформируемость в горизонтальном и вертикальном направлениях может быть разной (проявляется анизотропия).
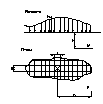
22. Метод статического зондирования. Зондированием грунта называется погружение в грунт конуса стандартного размера. Зондирование служит для оценки плотности песчаных грунтов и консистенции глинистых грунтов, выявления слабых прослоек грунта. При статическом зондировании измеряется усилие погружения (задавливания домкратом) конуса. В результате статического зондирования строятся графики зависимости удельного сопротивления погружению конуса с углом при вершине 60° в зависимости от глубины залегания грунтов, в которые он вдавливается. При этом боковое сопротивление погружению штанги, на которую насажен конус, исключается. После проведения зондирования выявляются слабые слои грунтов основания и дается не только качественная, но и количественная оценка сопротивления грунтов внедрению конуса Рисунок. Интерпретация результатов зондирования по глубине, м
23. Метод динамического зондирования. Зондированием грунта называется погружение в грунт конуса стандартного размера. Зондирование служит для оценки плотности песчаных грунтов и консистенции глинистых грунтов, выявления слабых прослоек грунта. При динамическом зондировании - количество ударов, необходимое для погружения конуса также на заданное расстояние по глубине. В результате динамического зондирования строятся графики зависимости количества ударов для погружения стандартного конуса (на 10 см) или пробоотборника в зависимости от залегания тех или иных пластов грунта. После проведения зондирования выявляются слабые слои грунтов основания и дается не только качественная, но и количественная оценка сопротивления грунтов внедрению конуса. Рисунок. Интерпретация результатов зондирования по глубине
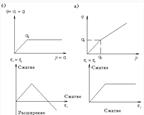
24.25.26. Сопротивление грунтов сдвигу. Методы опредления парамтров прочноти грунта. Закон Кулона для песчаных грунтов. Закон Кулона для связных грунтов. Сопротивление грунтов сдвигу определяет их прочность и устойчивость в основаниях сооружений и откосах, а также давления на ограждения котлованов. Сопротивление сдвигу по-разному проявляется в песчаных и глинистых грунтах и зависит от характера между частицами, слагающими грунт. Сопротивление грунта сдвигу может определяться различными методами: -метод прямого плоскостного среза; - -метод одноосного сжатия; - -метод трехосного сжатия; -метод лопостных испытаний; -метод шариковой пробы; Закон Кулона для песчаных грунтов имеет следующий вид: t = ×stgj Закон Кулона для связных грунтов имеет следующий вид: t = ×stgj + c. где φ- угол внутреннего трения. Угол внутреннего трения следует рассматривать как параметр линейного графика среза образца песчаного грунта, который проведен через начало координат. Рисунок. Результирующая схема испытания прямым срезом: а - песчаный грунт; б - глинистый грунт
27. Лопастное испытание грунтов на сдвиг. метод заключается в том, что лопастная крыльатка высотой h и диаметром d вдавливается в грунт, и вращением ее поверхности грунт срезается. Зная величину крутящего момента Мк соответствующего моменту среза грунта, вычисляем сопрот-е грунта сдвигу τS по ф-ле: τS=(2Мк)/(πd²h(1+d/3h). 28. Испытания грунтов в стабилометре и приборе с независимо регулиуемыми главными напряжениями. Сложное напряженное состояние с помощью компрессионных испытаний оценить нельзя. Большую определенность дают трехосные испытания в стабилометрах. Испытание грунта в приборе трехосного сжатия ближе отвечает его работе в природных условиях и даёт наиболее надёжные результаты в определении его прочностных и деформационных свойств. Трехосному напряженному состоянию грунт подвергается в стабилометре. В приборе грунт находится в условиях объёмного напряженного состояния. Особенностью таких испытаний в стабилометрах является равномерное боковое сжатие образца, т.е. равенство боковых главных напряжений. Для наблюдениея за деформировнием образца стенки камеры обычно изготавливаются из прозрачного материала. Оценка сжимаемости грунтов в приборах трехосного сжатия производится по объемной деформации грунта
29-30. Условие предельного равновесия: Условие предельного равновесия в главных напряжениях для сыпучего грунта:
31.Определение показателей сжимаемости по результатам испытаний в стабилометре. Сложное напряженное состояние с помощью компрессионных испытаний оценить нельзя. Большую определенность дают трехосные испытания в стабилометрах. Испытание грунта в приборе трехосного сжатия ближе отвечает его работе в природных условиях и даёт наиболее надёжные результаты в определении его прочностных и деформационных свойств. Трехосному напряженному состоянию грунт подвергается в стабилометре. В приборе грунт находится в условиях объёмного напряженного состояния. Особенностью таких испытаний в стабилометрах является равномерное боковое сжатие образца, т.е. равенство боковых главных напряжений. Для наблюдениея за деформировнием образца стенки камеры обычно изготавливаются из прозрачного материала. Оценка сжимаемости грунтов в приборах трехосного сжатия производится по объемной деформации грунта
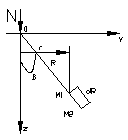
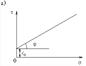
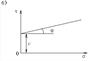
32.Структурно-фазовая деформируемость грунтов. Общая зависимость между деформациями и напряжениями. Рисунок При любой нагрузке грунта, как правило наблюдаются и восстанавливающие и остаточные деформации грунта. Зависимость в общем случае будет криволинейной, особенно если рассматривать деформации в большом диапазоне. Криволинейная зависимость между общими относительными деформациями е и напряжениями σ достаточно хорошо можно апроксимировать степенным законом. е=ασm 33. Принцип линейной деформируемости. Если зависимость между общими деформациями и напряжениями линейная, то для определения напряжений в грунтах полностью применимы уравнения теории упругости, для опделения же общих деформаций грунтов необходимы добавочные условия. Сформулированное положение носит название принцип линейной деформируемости грунтов. (При небольших изменених давления можно рассматривать грунт как линейно-деформируемое тела, т.е. с достаточной для практических целей точностью принимать зависимость между общими деформациями и напряжениями для них)-на этом положении базируется принцип линейной зависимости. 34. Определение напряжения в грунте от действия вертикальной сосредоточенной силы. От действия силы N во всех точках полупространства возникает сложное напряженное состояние. Пусть положение точки М1 определяется полярными координатами R и β системы координат с началом в точке приложения силы N. Под действием силы N точка М1 переместиться в направлении радиуса R на величину s1. Чем дальше от точки О будет расположена точка М1, тем меньше будет ее перемещение; при R=бесконечности перемещение точки М1будет =0.Следовательно S1 можно принять обратно пропорциональным R. В то же время при одном и том же значении R для различных величин угла β перемещения точек будут неодинаковы. Наибольшее перемещение получит точка, расположенная на оси z, т.е. при β=0. С увеличением угла β перемещения по направлению радиуса R уменьшаются, и в случае β=90 град. При малых деформациях будут =0.В связи с этим можно принять, что перемещение точки М1 по направлению радиуса, кроме зоны около точки приложения силы N, будет S1=(ά1/R)cosβ, где ά1-коэфф. пропорциональности. Эта зависимость удовлетворяет граничным условиям. Рассм. теперь точку М2 на продолжении радиуса R. Пусть точка М2 находиться на расстоянии dR от точки М1.Руководствуясь записанным выражением, найдем перемещение точки М2 по направлению радиуса R: S2=[ά1/(R+dR)]/cosβ. Ком случае относительная деформация грунта на отрезке dR составит
35. Определение напряжения в грунте от действия нескольких сосредоточенных сил. Если к поверхности изотропного линейно-деформируемого полупространства приложено несколько сил(N1,N2,…..Nn), то при прямой пропорциональности между напряжениями и деформациями можно использовать принцип суперпозиции и найти значение σz в любой точке М простым суммированием: σz= K1N1/z²+K2N2/z²+……+KnNn/z². Значение коэффициенте К определяют по таблицам в зависимости от отношений r1/z,r2/z,….., rn/z.
36 Определение напряжения в грунте от действия произвольной в плане распределенной нагрузки. Пусть к поверхности изотропного линейно-деформируемого полупространства в пределах площади приложено распределенное давление. Загруженную площадь можно разбить на небольшие прямоугольники со сторонами b и l и более сложные фигуры по контуру. С некоторым приближением давление, распределенное в пределах i-го прямоугольника, можно заменить равнодействующей Ni, приложенной в центре тяжести этого давления. Вертикальное сжимающее напряжение от действия силы Ni составит σzi= KiNi/z². Определив величину σzi от нагрузки каждой из небольших фигур, на которые разбита площадь А, и произведя суммирование этих напряжений, определим напряжение σz от действия распределенной местной нагрузки: σz= Σ KiNi/z² Точность расчета увеличивается с уменьшением b и l
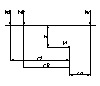
37. Определение напряжений в грунте по методу угловых точек под центром загруженной площадки. Метод угловых точек удобен для вычисления напряжений под центром равномерно загруженной площадки. На глубине z под центром площадки размерами lxb (l>b) напряжение равно сумме ответствующих угловых напряжений, создаваемых четырьмя площадками размерами l/2*b/2. Так, σя=Kop, где Ко=4Ку для площадки размерами и относительной вертикальной координаты β=2z/b. Значения коэф-в К приводятся в таблице
|

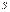 , см, от нагрузки
, см, от нагрузки 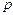 , МПа, устанавливается модуль деформации
, МПа, устанавливается модуль деформации 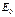 . Основным достоинством этого вида испытаний является то, что они ведутся непосредственно в грунтовом массиве. При испытаниях жесткими штампами требуется тщательная их установка на грунт с прилеганием по всей поверхности. Штамповые испытания производятся также в скважинах. В этом случае штамп устанавливается в забое скважины. Применяются также винтовые штампы.
. Основным достоинством этого вида испытаний является то, что они ведутся непосредственно в грунтовом массиве. При испытаниях жесткими штампами требуется тщательная их установка на грунт с прилеганием по всей поверхности. Штамповые испытания производятся также в скважинах. В этом случае штамп устанавливается в забое скважины. Применяются также винтовые штампы.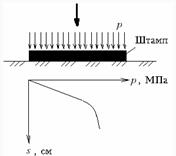



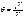 где
где 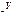 - изменение объема образца.В стабилометрах изменение объема образца определяется по объему жидкости, поступающей в камеру прибора или входящей из нее.
- изменение объема образца.В стабилометрах изменение объема образца определяется по объему жидкости, поступающей в камеру прибора или входящей из нее.
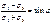 или
или 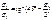 для связного грунта:
для связного грунта: 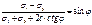 или
или 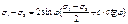

 где
где 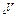 - изменение объема образца. В стабилометрах изменение объема образца определяется по объему жидкости, поступающей в камеру прибора или входящей из нее.
- изменение объема образца. В стабилометрах изменение объема образца определяется по объему жидкости, поступающей в камеру прибора или входящей из нее.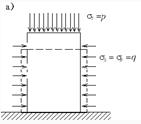
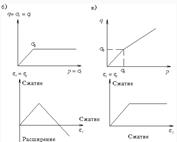
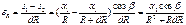 . Пренебрегая величиной RdR, малой по сравнению с R², и учитывая линейную зависимость между напряжениями и деформациями, найдем выражение для напряжений сжатия, действующих на площадки, перпендикулярные направлению радиуса R, без учета силы тяжести грунта:
. Пренебрегая величиной RdR, малой по сравнению с R², и учитывая линейную зависимость между напряжениями и деформациями, найдем выражение для напряжений сжатия, действующих на площадки, перпендикулярные направлению радиуса R, без учета силы тяжести грунта: 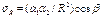 , где ά2-коэфф. пропорциональности между напряжениями и деформациями. Учитывая, что R²=r²+z²,будем иметь
, где ά2-коэфф. пропорциональности между напряжениями и деформациями. Учитывая, что R²=r²+z²,будем иметь 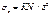 , где
, где 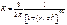 Аналогично могут быть найдены остальные компоненты напряжения в точке М1.Подставляя в последнюю формулу значение коэфф. К найденного по таблице определяют вертикальное сжимающее напряжение σz, развивающееся в грунтах при действии сосредоточенной стлы.
Аналогично могут быть найдены остальные компоненты напряжения в точке М1.Подставляя в последнюю формулу значение коэфф. К найденного по таблице определяют вертикальное сжимающее напряжение σz, развивающееся в грунтах при действии сосредоточенной стлы.