Зависимости амплитуды вынужденных колебаний и сдвига фаз от частоты внешнего воздействия.
1. Вернемся к механической системе пружинного маятника, на который действует внешняя сила, изменяющаяся по гармоническому закону. Для такой системы дифференциальное уравнение и его решение соответственно имеют вид:
Проанализируем зависимость амплитуды колебаний и сдвига фаз от частоты внешней вынуждающей силы, для этого найдем первую и вторую производную от х и подставим в дифференциальное уравнение.
Воспользуемся методом векторной диаграммы. Из уравнения видно, что сумма трех колебаний в левой части уравнения (Рисунок 4.1) должна быть равна колебанию в правой части. Векторная диаграмма выполнена для произвольного момента времени t. Из нее можно определить
Рисунок 4.1
Учитывая значение
2. Исследуем зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы и величины силы сопротивления в колеблющейся механической системе, по этим данным построим график РЕЗОНАНС. Явление резкого возрастания амплитуды вынужденных колебаний при частоте вынуждающей силы, равной
Кривые на Рисунке 4.2 отражают зависимость
Рисунок 4.2 – Графики зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы. 3. Используем данные об амплитуде и сдвиге фаз вынужденных колебаний для механической системы и выразим эти же характеристики для аналогичных величин электромагнитной системы (LCR– контур с включенным в его цепь внешним источником ЭДС, величина которой изменяется по гармоническому закону):
5. Сила тока при установившихся в контуре колебаниях равна:
где
График зависимости
Графическое изображение гармонических колебаний. Биение. Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты
воспользовавшись методом вращающегося вектора амплитуды. Построим векторные диаграммы этих колебаний (рис. 203). Tax как векторы A1 и А2 вращаются с одинаковой угловой скоростью w0, то разность фаз (j 2 —j 1)между ними остается постоянной. Очевидно, что уравнение результирующего колебания будет
В выражении (144.1) амплитуда А и начальная фаза j соответственно задаются соотношениями
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (j 2 —j 1) складываемых колебаний. Проанализируем выражение (144.2) в зависимости от разности фаз (j 2 —j 1): 1) j 2 —j 1 = ±2 mp (т= 0, 1, 2,...), тогда A=A 1 +A 2, т. е. амплитуда результирующего колебания А равнасумме амплитуд складываемых колебаний; 2) j 2 —j 1 = ±(2 m +1) p (т= 0, 1, 2,...), тогда A= | A 1 –A 2|, т. е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний. Для практики особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями. Пусть амплитуды складываемых колебаний равны А, а частоты равны w и w +D w, причем D w << w. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:
Складывая эти выражения и учитывая, что во втором сомножителе D w /2<< w, найдем
Результирующее колебание (144.3) можно рассматривать как гармоническое с частотой w, амплитуда А б, которого изменяется по следующему периодическому закону:
Частота изменения А б в два раза больше частоты изменения косинуса (так как берется по модулю), т. е. частота биений равна разности частот складываемых колебаний:
Период биений
Характер зависимости (144.3) показан на рис. 204, где сплошные жирные линии дают график результирующего колебания (144.3), а огибающие их — график медленно меняющейся по уравнению (144.4) амплитуды. Определение частоты тона (звука определенной высоты) биений между эталонным и измеряемым колебаниями — наиболее широко применяемый на практике метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т. д. Любые сложные периодические колебания s = f (t) можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, кратными циклической частоте w0:
Представление периодической функции в виде (144.5) связывают с понятием гармонического анализа сложного периодического колебания,или разложения Фурье. *Слагаемые ряда Фурье, определяющие гармонические колебания с частотами w0, 2w0, 3w0,..., называются первой (или основной), второй, третьей и т. д. гармониками сложного периодического колебания. * Ж. Фурье (1768—1830) — французский ученый.
Сложение взаимно перпендикулярных колебаний. Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем это в виде
где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как
и заменяя во втором уравнении
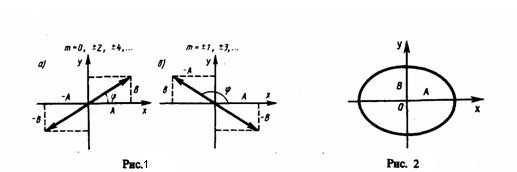
Поскольку траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными. Размеры осей эллипса и его ориентация зависят от амплитуд складываемых колебаний и разности фаз α. Рассмотрим некоторые частные случаи, которые представляют для нас физический интерес: 1) α = mπ (m=0, ±1, ±2,...). В этом случае эллипс становится отрезком прямой
где знак плюс соответствует нулю и четным значениям m (рис. 1а), а знак минус — нечетным значениям m (рис. 2б). Результирующее колебание есть гармоническое колебание с частотой ω и амплитудой, которое совершается вдоль прямой (3), составляющей с осью х угол. В этом случае имеем дело с линейно поляризованными колебаниями; 2) α = (2m+1)(π/2) (m=0, ± 1, ±2,...). В этом случае уравнение станет иметь вид
Это есть уравнение эллипса, у которого оси совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 2). Если А=В, то эллипс (4) превращается в окружность. Такие колебания называются циркулярно поляризованными колебаниями или колебаниями, поляризованными по кругу.
Если частоты складываемых взаимно перпендикулярных колебаний имеют различные значения, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих замкнутых кривых зависит от соотношения амплитуд, разности фаз и частот складываемых колебаний. На рис. 3 даны фигуры Лиссажу для различных соотношений частот (даны слева) и разностей фаз (даны вверху; разность фаз равна φ). Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, которые параллельны осям координат. По виду фигур можно найти неизвестную частоту по известной или найти отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу — широко применяемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.
|

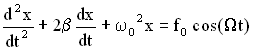 ,
,  .
.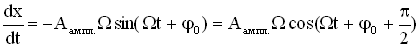 ,
, ,
,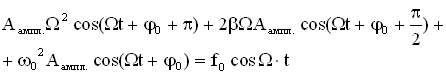
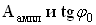 .
.
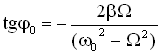 ,
,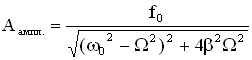 .
. ,
,  ,
,  , получим формулы для φ0 и Аампл. механической системы:
, получим формулы для φ0 и Аампл. механической системы: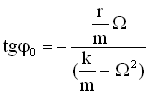 ,
, .
. . Результаты исследования отражены в Рисунке 4.2, по ним видно, что при некоторой частоте вынуждающей силы
. Результаты исследования отражены в Рисунке 4.2, по ним видно, что при некоторой частоте вынуждающей силы  амплитуда колебаний резко возрастает. И это возрастание тем больше, чем меньше коэффициент затухания β. При
амплитуда колебаний резко возрастает. И это возрастание тем больше, чем меньше коэффициент затухания β. При  амплитуда колебаний становится бесконечно большой
амплитуда колебаний становится бесконечно большой  .
.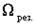 , называется резонансом.
, называется резонансом.
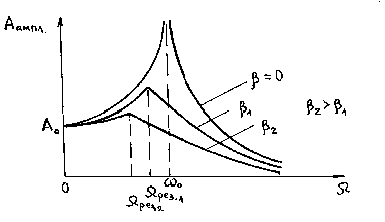
 ,
,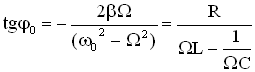 .
. ,
, - амплитуда силы тока, ψ0 – сдвиг фаз между силой тока и внешнейЭДС в контуре. Амплитуда силы тока и ψ0 находятся по формулам:
- амплитуда силы тока, ψ0 – сдвиг фаз между силой тока и внешнейЭДС в контуре. Амплитуда силы тока и ψ0 находятся по формулам: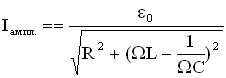 ,
,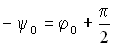 ,
,  .
.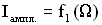 представлен на Рисунке 4.3.
представлен на Рисунке 4.3.
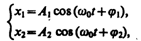
 (144.1)
(144.1)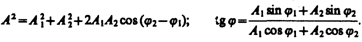 (144.2)
(144.2)
 (144.3)
(144.3) (144.4)
(144.4)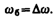
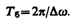
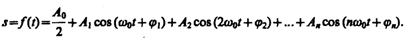 (144.5)
(144.5)
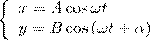 (1)
(1)
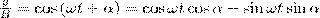
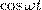 на
на 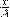 и
и 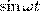 на
на  , найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей:
, найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей: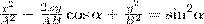 (2)
(2) (3)
(3)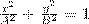 (4)
(4)