Свободные гармонические колебания.
Гармонические колебания - периодический процесс, в котором рассматриваемый параметр изменяется по гармоническому закону. Если на колебательную систему не действуют внешние переменные силы, то такие колебания называются свободными. Рассмотрим массу, которая колеблется на пружине как показано на рисунке. Если амплитуда колебаний мала, то координата x массы по вертикальной оси изменяется по гармоническому закону: x = A sin(w t + j) где A - амплитуда колебаний, t - время, j - фаза колебаний,w- угловая частота колебаний,w= 2 p f = 2 p / T, f - частота колебаний, T - период колебаний. Далее мы найдём период колебаний T пружинного маятника, состоящего из грузика массой m и пружины жёсткостью k. Если грузик смещён из нулевого положения (в котором пружина не деформирована) на расстояние x, то на грузик со стороны пружины будет действовать сила- kx. Помимо этого на грузик действует сила тяжести mg. Согласно второму закону Ньютона, сумма всех сил, приложенных к грузику, равна ma, где a - ускорение. Таким образом, мы можем записать дифференциальное уравнение для пружинного маятника: m d2 x /d t 2 = - kx + mg где g - ускорение свободного падения в гравитационном поле,d2 x /d t 2 - вторая производная координаты x по времени t. Это уравнение имеет следующее решение: x = A sin[(k / m)1/2 t + j] + mg / k Мы можем видеть из этой формулы, что период колебаний равен T = 2p(m / k)1/2 и, соответственно, угловая частота w равна w = (k / m)1/2 Амплитуда колебаний A и фаза колебаний j зависят от начальных условий (в момент времени t =0): начального смещение грузика x 0 и начальной скорости v 0. В состоянии равновесия пружина растянута на величину mg / k. Предположим, что колеблющийся грузик связан с пером, который рисует линию на бумажной ленте. Если лента движется равномерно в горизонтальном направлении, то перо будет рисовать на ней синусоиду. Зная скорость движения ленты и период синусоиды, мы можем вычислить период колебаний грузика на пружине. В общем случае на осциллятор действует сила трения, пропорциональная скорости движения грузика: F=av. В случае пружинного маятника эта сила возникает из-за сопротивления воздуха и неупругих свойств самого материала, из которых изготовлена пружина. В результате, амплитуда колебаний будет со временем уменьшаться. Уравнение свободного гармонического осциллятора с затуханием может быть записано следующим образом: m (d2 x /d t 2) + a (d x /d t) + kx = mg где a - коэффициент трения. Это уравнение может быть переписано в виде d2 x /d t 2+ 2g(d x /d t) + W2 x = g где 2g = a / m; W2= k / m В случае, когда W2 > g2 уравнение колебаний свободного гармонического осциллятора с затуханием имеет следующее решение: x = A e-g t cos(w t + j) При этом период колебаний зависит от коэффициента затухания g: T = 2p/w= 2p/(W2 -g2)1/2 Дифференциальное уравнение гармонических колебаний и его решение. Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на систему, которая совершает колебания. Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Исследование гармонических колебаний важно по двум причинам: 1) колебания, которые встречаются в природе и технике, часто имеют близкий к гармоническому характер; 2) различные периодические процессы (процессы, которые повторяются через равные промежутки времени) можно представить как суперпозицию (наложение) гармонических колебаний. Гармонические колебания некоторой величины s описываются уравнением вида
где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А. Определенные состояния системы, которая совершает гармонические колебания, повторяются через промежуток времени Т, имеющий название период колебания, за который фаза колебания получает приращение (изменение) 2π, т. е.
откуда
Величина, обратная периоду колебаний,
т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем
Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса. Найдем первую и вторую производные по времени от величины s, совершающей гармонические колебания:
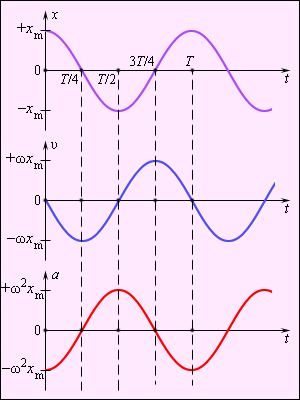
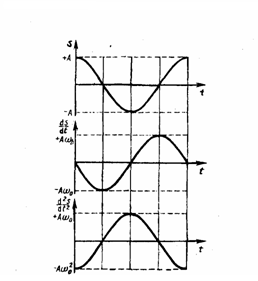
т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин в формулах (4) и (5) соответственно равны Аω0 и Аω02. Фаза величины в формуле (4) отличается от фазы величины в формуле (1) на π/2, а фаза величины в выражении (5) отличается от фазы величины (1) на π. Значит, в моменты времени, когда s=0, ds/dt имеет наибольшие значения; когда же s становится равным максимальному отрицательному значению, то d2s/dt2 равен наибольшему положительному значению (рис. 1).
Рис.1
Из выражения (5) непосредственно вытекает дифференциальное уравнение гармонических колебаний
(где s = A cos(ω0t+φ)). Решением данного дифференциального уравнения является выражение (1). Смещение, скорость и ускорение материальной точки при гармонических колебаниях и их графики На рис. 2.1.4 приведены графики координаты, скорости и ускорения тела, совершающего гармонические колебания. Гармоническое колебание описывается формулой, выражающей Скорость - производная от смещения: v=x'=Aw cos(wt+f).
|

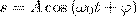 (1)
(1)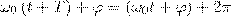
 (2)
(2) (3)
(3)
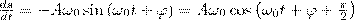 (4)
(4)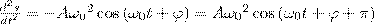 (5)
(5)
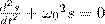 (6)
(6)