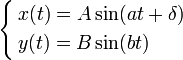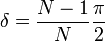Фигуры Лиссажу.
Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или Математическое выражение для кривой Лиссажу [править]
где A, B — амплитуды колебаний, a, b — частоты, δ; — сдвиг фаз Вид кривой сильно зависит от соотношения a / b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности(A = B, δ; = π/2 радиан) и отрезка прямой (δ; = 0). Ещё один пример фигуры Лиссажу — парабола (a / b = 2, δ; = π/2). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии a / b — рациональное число. Фигуры Лиссажу, где a = 1, b = N (N — натуральное число) и
являются полиномами Чебышева первого рода степени N.
|
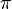вырождаются в отрезки прямых, а при разности фаз 
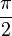и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.
