Добротность
Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины. Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими. Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения
где r - коэффициент сопротивления среды. Знак минус показывает, что FC направлена в сторону противоположную скорости. Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r. По второму закону Ньютона
где β - коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.
- дифференциальное уравнение затухающих колебаний.
- уравнение затухающих колебаний. ω – частота затухающих колебаний:
Период затухающих колебаний:
Если затухания выражены слабо (β→0), то рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону
В уравнении (1) А0 и φ0 - произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания
Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз
τ - время релаксации. Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D, который равен отношению амплитуд, отстоящих по времени на период:
Логарифмический декремент затухания равен логарифму D:
Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в е раз. Логарифмический декремент затухания - постоянная для данной системы величина. Еще одной характеристикой колебательной система является добротность Q.
Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ. Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии. Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.
Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим. 1. Коэффициент затухания β. Изменение амплитуды затухающих колебаний происходит по экспоненциальному закону:
Пусть за время τ амплитуда колебаний уменьшится в "e " раз ("е" – основание натурального логарифма, е ≈ 2,718). Тогда, с одной стороны,
Промежуток времени τ, за который амплитуда уменьшается в "е" раз, называется временем релаксации. энергия затухающих колебаний------------------
|

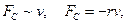
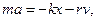
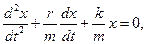



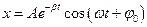
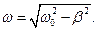

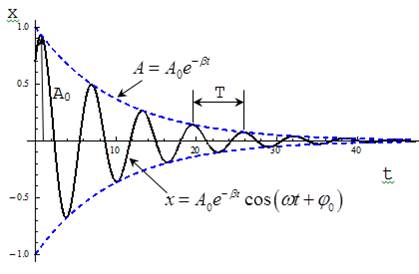 Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно говорить, когда β мало.
Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно говорить, когда β мало.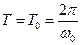 . Затухающие колебания можно
. Затухающие колебания можно

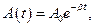
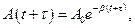

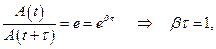

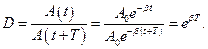

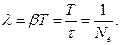
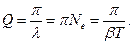
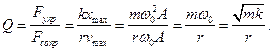
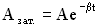 .
. , а с другой стороны, расписав амплитуды Азат.(t) и Азат.(t+τ), имеем
, а с другой стороны, расписав амплитуды Азат.(t) и Азат.(t+τ), имеем 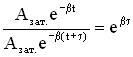 . Из этих соотношений следует βτ = 1, отсюда
. Из этих соотношений следует βτ = 1, отсюда .
.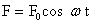 , то в системе устанавливаются гармонические колебания с частотой внешней вынуждающей силы (процесс установления колебаний изображен на рисунке: вынужденные колебания накладываются на свободные затухающие колебания; после того, как свободные колебания прекращаются, остаются только вынужденные).
, то в системе устанавливаются гармонические колебания с частотой внешней вынуждающей силы (процесс установления колебаний изображен на рисунке: вынужденные колебания накладываются на свободные затухающие колебания; после того, как свободные колебания прекращаются, остаются только вынужденные).




