Скорость распространения волныВ том, что распространение механических волн происходит не мгновенно, нас убеждают простейшие наблюдения. Каждый видел, как постепенно и равномерно расширяются круги на воде или как бегут морские волны. Здесь мы непосредственно видим, что распространение колебаний из одного места в другое занимает определенное время. Но и для звуковых волн, которые в обычных условиях невидимы, легко обнаруживается то же самое. Если вдали происходит гроза, выстрел, взрыв, свисток паровоза, удар топора и т. п., то мы сначала видим эти явления и лишь спустя известное время слышим звук (рис. 63). Чем дальше от нас источник звука, тем больше запаздывание. Промежуток времени между вспышкой молнии и ударом грома может доходить иногда до нескольких десятков секунд. Зная расстояние от источника звука и измерив запаздывание звука, можно определить скорость его распространения. В сухом воздухе при температуре 10 °С эта скорость оказалась равной 337,5 м/с. Для сравнения напомним, что современные самолеты могут развивать скорости, превышающие скорость звука в воздухе (так называемые сверхзвуковые скорости), а артиллерийские снаряды летят со скоростями 1,5 км/с и более. Скорость ракет, выводящих на орбиту искусственные спутники Земли, должна достигать значений, превышающих 8 км/с. Энергия бегущей волны. Упругая среда, в которой распространяется волна, обладает как кинетической энергией колебательного движения частиц так и потенциальной энергией, обусловленной деформацией среды. Можно показать, что объемная плотность энергии для плоской бегущей гармонической волны (5)
где r =dm/dV - плотность среды, т.е. периодически изменяется от 0 до r А2w2 за время p /w=Т/2. Среднее значение плотности энергии за промежуток времени p /w=Т/2
Для характеристики переноса энергии вводят понятие вектора плотности потока энергии
Если через площадку D S^, перпендикулярную к направлению распространения волны, переносится за время D t энергия DW, то плотность потока энергии Рис. 2
где D V=DS^ uDt - объем элементарного цилиндра, выделенного в среде. Поскольку скорость переноса энергии или групповая скорость есть вектор, то и плотность потока энергии можно представить в виде вектора
Этот вектор ввел профессор Московского университета Н.А. Умов в 1874 г. Среднее значение его модуля называют интенсивностью волны
Для гармонической волны u =v[cм.(14)], поэтому для такой волны в формулах (17)-(19) u можно заменить на v. Вектор Умова. Если на пути распространения волны поставить некоторую площадку dS, то в этом случае говорят о потоке энергии через эту площадку. Отношение энергии, переносимой сквозь некоторую площадку к промежутку времени, за который произошел ее перенос, называют потоком энергии. Согласно определению можно записать формулу потока энергии:
Используя объемную плотность энергии w, запишем полную энергию волны dW= w (vdt) dS сos a, где ℓ = vdt - расстояние, на которое перемещается волна, имея скорость v за малое время dt; a - угол между векторами скорости и нормали к площадке (рис. 7.6)
Рис. 7.6 или
где Следовательно, поток энергии переносимый волной
или
где
называют вектором Умова-Пойнтинга, или вектором плотности потока энергии. Вывод: Модуль вектора Умова-Пойнтинга характеризует плотность потока энергии волны, переносимой через площадку перпендикулярно направлению распространению волны т.е., Принцип суперпозиции волн. Принцип суперпозиции (наложения) волн заключается в следующем: в линейных средах волны распространяются независимо друг от друга, то есть волна не изменяет свойства среды, и другая волна распространяется так, будто первой волны нет. Это позволяет вычислять итоговую волну как сумму всех волн, распространяющихся в данной среде. При сложении двух или более синусоидальных волн результирующая волна в общем случае уже не будет синусоидальной. Рассмотрим в качестве примера результат сложения двух плоских однонаправленных волн с одинаковыми амплитудами и разными, но близкими частотами и волновыми числами:
Полученная волна не является синусоидальной, так как величина перед синусом (амплитуда волны) меняется со временем и координатой. Однако, если на длине волны (и в течении периода) её изменения малы (что имеет место при малых dk и dw), волна ещё похожа на синусоиду; её иногда называют квазисинусоидальной. График этой волны представляет собой то, что мы в теории колебаний назвали биениями; однако здесь, в отличие от маятника, биения происходят не только во времени, но и в пространстве. Когерентность Когерентность волны означает, что в различных точках волны осцилляции происходят синхронно, то есть разность фаз между двумя точками не зависит от времени. Отсутствие когерентности, следовательно — ситуация, когда разность фаз между двумя точками не постоянна, а меняется со временем. Такая ситуация может иметь место, если волна была сгенерирована не единым излучателем, а совокупностью одинаковых, но независимых (то есть нескоррелированных) излучателей. Изучение когерентности световых волн приводит к понятиям временно́й и пространственной когерентности. При распространении электромагнитных волн в волноводахмогут иметь место фазовые сингулярности. В случае волн на воде когерентность волны определяет так называемая вторая периодичность. Без когерентности невозможно наблюдать такое явление, как интерференция. Интерференция и дифракция волн.
Если в среде распространяется несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Волны накладываются друг на друга, не возмущая (не искажая друг друга). Это и есть принцип суперпозиции волн. Если две волны, приходящие в какую-либо точку пространства, обладают постоянной разностью фаз, такие волны называются когерентными. При сложении когерентных волн возникает явление интерференции. Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении от преград. Напишем уравнения двух плоских волн, распространяющихся в противоположных направлениях (начальная фаза):
Сложим уравнения и преобразуем по формуле суммы косинусов (5.4.3): . Т.к., то можно записать: . Учитывая, что, получим уравнение стоячей волны:
В выражении для фазы не входит координата, поэтому можно записать:
где суммарная амплитуда. В точках, где координаты удовлетворяют условию (n = 1, 2, 3, …),, суммарная амплитуда равна максимальному значению:, – это пучности стоячей волны. Координаты пучностей:
В точках, координаты которых удовлетворяют условию (n = 0, 1, 2,…), и суммарная амплитуда колебаний равна нулю, – это узлы стоячей волны. Координаты узлов:
Точки среды, находящиеся в узлах, колебаний не совершают. Образование стоячих волн наблюдают при интерференции бегущей и отраженных волн. На границе, где происходит отражение волны, получается пучность, если среда, от которой происходит отражение, менее плотная (рис. 5.5, а), и узел – если более плотная (рис. 5.5, б). Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях. Звуковые волны. Под звуком понимают упругие волны среды, воспринимаемые ухом человека. Опыт показывает, что наше ухо воспринимает как звук механические колебания, частота которых лежит в пределах от 20 Гц до 20 кГц. Упругие волны с частотой менее 20 Гц называются инфразвуком, с частотой более 20 кГц - ультразвуком. Звук может распространяться в виде продольных и поперечных волн. В газообразной и жидкой фазе возникают только продольные волны, в твердых телах, помимо продольных, возникают также и поперечные волны. В зависимости от структуры спектра колебания среды различают шумы и музыкальные звуки. Шумы - это непериодические колебания. Им соответствует сплошной спектр, т. е. набор частот, непрерывно заполняющих некоторый интервал. Музыкальные звуки обладают линейчатым спектром с кратными частотами, следовательно, они представляют собой периодические колебания. Для слушающего человека сразу становятся очевидными две характеристики звука, а именно его громкость и высота тона. Каждой из этих субъективных характеристик соответствует величина, измеряемая физическими методами. Громкость связана с энергией звуковой волны, которая представляет продольные колебания воздуха. Согласно уравнению (4.8) энергия волны пропорциональна квадрату амплитуды. Человеческое ухо способно воспринимать звуки с интенсивностью вплоть до 10-12 Вт/м2 (порог слышимости) и до 1 Вт/м2 (так называемый порог болевого ощущения). Громкость зависит также от частоты звука. Поэтому величина, которую мы воспринимаем, как громкость, не прямо пропорциональна интенсивности. Но, чем больше интенсивность, тем звук громче. Высота тона звука определяется частотой упругих колебаний, воспринимаемых ухом. Звук характеризуется тембром. Тембр звука, или иногда называют его окраской звука, определяется амплитудами и частотой дополнительных обертонов (звуки более высокой частоты). На основной тон могут накладываться обертоны с различными амплитудами, что и определяет тембр звука. Скорость звука в газах. Скорость в газах. В газах возможен только один тип деформации: сжатие – разрежение. Соответствующий модуль упругости В называется модулем объемной деформации. Он определяется соотношением –D P = B (D V / V). Здесь D P – изменение давления, D V / V – относительное изменение объема. Знак «минус» показывает, что при увеличении давления объем уменьшается. Величина В зависит от того, изменяется или нет температура газа при сжатии. В случае звуковой волны можно показать, что давление изменяется очень быстро и теплота, выделяющаяся при сжатии, не успевает уходить из системы. Таким образом, изменение давления в звуковой волне происходит без теплообмена с окружающими частицами. Такое изменение называется адиабатическим. Установлено, что скорость звука в газе зависит только от температуры. При данной температуре скорость звука примерно одинакова для всех газов. При температуре 21,1° С скорость звука в сухом воздухе составляет 344,4 м/с и возрастает с повышением температуры. Шкала уровней звука. изическая характеристика громкости звука - уровень звукового давления, в децибелах (дБ). «Шум» - это беспорядочное смешение звуков. Звуки с низкой и высокой частотой кажутся тише, чем среднечастотные той же интенсивности. С учётом этого, неравномерную чувствительность человеческого уха к звукам разных частот модулируют с помощью специального электронного частотного фильтра, получая, в результате нормирования измерений, так называемый эквивалентный (по энергии, "взвешенный") уровень звука с размерностью дБА (дБ(А), то есть - с фильтром "А"). Человек, в дневное время суток, может слышать звуки громкостью от 10-15 дБ и выше. Максимальный диапазон частот для человеческого уха, в среднем - от 20 до 20 000 Гц (возможный разброс значений: от 12-24 до 18000-24000 герц). В молодости - лучше слышен среднечастотный звук с частотой 3 КГц, в среднем возрасте - 2-3КГц, в старости - 1КГц. Такие частоты, в первые килогерцы (до 1000-3000 Гц - зона речевого общения) - обычны в телефонах и по радио на СВ и ДВ диапазонах. С возрастом, воспринимаемый на слух звуковой диапозон сужается: для высокочастотных звуков - уменьшаясь до 18 килогерц и менее (у пожилых людей, каждые десять лет - примерно на 1000Гц), а для низкочастотных - увеличиваясь от 20 Гц и более. У спящего человека, основным источником сенсорной информации об окружающей обстановке - становятся уши ("чуткий сон"). Чувствительность слуха, ночью и при закрытых глазах - увеличивается на 10-14 дБ (до первых децибел, по шкале дБА), по сравнению с дневным временем суток, поэтому - громкий, резкий шум с большими скачками громкости, может разбудить спящих людей. В случае отсутствия на стенах помещений звукопоглощающих материалов (ковров, специальных покрытий), звук будет громче из-за многократного отражения (реверберации, то есть - эха от стен, потолка и мебели), что увеличит уровень шума на несколько децибел.
Интенсивность и громкость звука. Интенсивность звука (абсолютная) — величина, равная отношению потока звуковой энергии dP через поверхность, перпендикулярную направлению распространениязвука, к площади dS этой поверхности:
Единица измерения — ватт на квадратный метр (Вт/м2).
где ZS — удельное акустическое сопротивление среды. Гро́мкость зву́ка — субъективное восприятие силы звука (абсолютная величина слухового ощущения). Громкость главным образом зависит от звукового давления,амплитуды и частоты звуковых колебаний. Также на громкость звука влияют его спектральный состав, локализация в пространстве, тембр, длительность воздействия звуковых колебаний и другие факторы[1][2]. Единицей абсолютной шкалы громкости является сон. Громкость в 1 сон — это громкость непрерывного чистого синусоидального тона частотой 1 кГц, создающегозвуковое давление 2 мПа.
|
(14)
. (16)
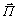- вектор Умова.
Выведем выражение для него.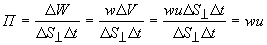
, (17)
, Вт/м2 (18)
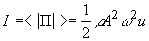(19)
.
,
.
,
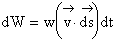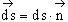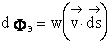
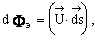
