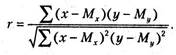Коэффициент корреляции

Выявление взаимосвязей. Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между некоторыми наблюдаемыми переменными. Знание взаимозависимостей отдельных признаков дает возможность решать одну из кардинальных задач любого научного исследования: возможность предвидеть, прогнозировать развитие ситуации при изменении конкретных характеристик объекта исследования. Например, основное содержание любой экономической политики в конечном счете может быть сведено к регулированию экономических переменных, осуществляемому на базе выявленной тем или иным образом информации об их взаимовлиянии. Поэтому проблема изучения взаимосвязей показателей различного рода является одной из важнейших в статистическом анализе.

Обычно взаимосвязь между выборками носит не функциональный, а вероятностный (или стохастический) характер. В этом случае нет строгой, однозначной зависимости между величинами. При изучении стохастических зависимостей различают корреляцию и регрессию.

Регрессионный анализ (см. раздел «Регрессионный анализ») устанавливает формы зависимости между случайной величиной Y и значениями одной или нескольких переменных величин.

Корреляционный анализ состоит в определении степени связи между двумя случайными величинами X и Y. В качестве меры такой связи используется коэффициент корреляции. Коэффициент корреляции оценивается по выборке объема п связанных пар наблюдений (x_i,y_i) из совместной генеральной совокупности X и Y. Существует несколько типов коэффициентов корреляции, применение которых зависит от предположений о совместном распределении величин X и Y.

Для оценки степени взаимосвязи наибольшее распространение получил коэффициент линейной корреляции (Пирсона), предполагающий нормальный закон распределения наблюдений.

Коэффициент корреляции (R, r) — параметр, характеризующий степень линейной взаимосвязи между двумя выборками. Коэффициент корреляции изменяется от -1 (строгая обратная линейная зависимость) до 1 (строгая прямая пропорциональная зависимость). При значении 0 линейной зависимости между двумя выборками нет. Здесь под прямой зависимостью понимают зависимость, при которой увеличение или уменьшение значения одного признака ведет, соответственно, к увеличению или уменьшению второго. Например, при увеличении температуры возрастает давление газа, а при уменьшении — снижается (при постоянном объёме). При обратной зависимости увеличение одного признака приводит к уменьшению второго и наоборот. Примером обратной корреляционной зависимости может служить связь между температурой воздуха на улице и количеством топлива, расходуемого на обогрев помещения.

Выборочный коэффициент линейной корреляции между двумя случайными величинами X и Y рассчитывается по формуле

Коэффициент корреляции является безразмерной величиной и его значение не зависит от единиц измерения случайных величин X и Y.

Да практике коэффициент корреляции принимает некоторые промежуточные значения между 1 и -1 (рис. 1). Для оценки степени взаимосвязи можно руководствоваться следующими эмпирическими правилами. Если коэффициент корреляции (r) по абсолютной величине (без учета знака) больше, чем 0,95, то принято считать, что между параметрами существует практически линейная зависимость (прямая — при положительном r и обратная — при отрицательном (r). Если коэффициент корреляции |r| лежит в диапазоне от 0,8 до 0,95, говорят о сильной степени линейной связи между параметрами. Если 0,6 < | r | < 0,8, говорят о наличии линейной связи между параметрами. При | r| < 0,4 обычно считают, что линейную взаимосвязь между параметрами выявить не удалось.

Рис. 1. Примеры прямой (r = 0,7, а) и обратной (r=0,8, б) корреляционной зависимости

В MS Excel для вычисления парных коэффициентов линейной корреляции используется специальная функция КОРРЕЛ. Параметрами функции являются К0РРЕЛ(люс- сив1;массив2), где: массив1 — это диапазон ячеек первой случайной величины;

О массив2 — это второй интервал ячеек со значениями второй случайной величины.

Пример 1. Имеются результаты семимесячных наблюдений реализации путевок двух туристских маршрутов тура А и тура В.

Необходимо определить, имеется ли взаимосвязь между количеством продаж путевок обоих маршрутов.

Решение. Для выявления степени взаимосвязи прежде всего необходимо ввести данные в рабочую таблицу. Откройте новую рабочую таблицу. Введите в ячейку А1 слова Тур А. Затем в ячейки А2:А8 — соответствующие значения числа продаж. В ячейки B1B8 введите название и значения для тура В. Затем вычисляется значение коэффициента корреляции между выборками. Для этого табличный курсор установите в свободную ячейку (А9). На панели инструментов нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию КОРРЕЛ, после чего нажмите кнопку ОК. Появившееся диалоговое окно КОРРЕЛ за серое поле мышью отодвиньте вправо на 1-2 см от данных (при нажатой левой клавише). Указателем мыши введите диапазон данных Тур А в поле Массив 1 (А2;А8). В поле Массив 2 введите диапазон данных Тур В (В2:В8). Нажмите кнопку ОК. В ячейке А9 появится значение коэффициента корреляции — 0,995493. Значение коэффициента корреляции больше чем 0,95. Значит, можно говорить о том, что в течение периода наблюдения имелась высокая степень прямой линейной взаимосвязи между количествами проданных путевок обоих маршрутов (r = 0,995493).