Потоки в сетях
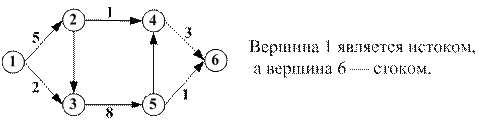
В этом разделе рассматриваются задача максимизации потока некоторого продукта по сети. Подобного рода задачи возникают при организации перекачки нефти или газа по трубопроводам, железнодорожного или автомобильного движения, передачи информации по сетям и т.д. Приведём необходимые определения, формализующие соответствующие предметные области. Сетью называется орграф без циклов с помеченными вершинами и дугами. Числа, которыми помечаются дуги сети, называются пропускными способностями дуг. Примеры вершин сети: перекрёстки дорог, телефонные узлы, железнодорожные узлы, аэропорты, склады и т.д. Примеры дуг сети: дороги, трубы, телефонные и железнодорожные линии и т.д. Сеть, у которой существует ровно один исток [3] и один сток [4], называется транспортной сетью. Пример транспортной сети:
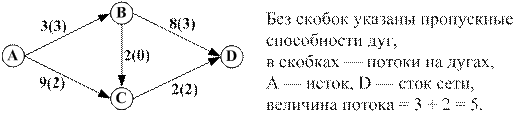
Потоком в транспортной сети называется неотрицательная функция, определённая на множестве дуг сети, удовлетворяющая двум условиям: 1) величина потока по каждой дуге не превосходит её пропускной способности; 2) сумма потоков, входящих в каждую вершину сети, за исключением истока и стока, равна сумме потоков, выходящих из вершины. Величина потока есть сумма потоков, выходящих из истока, или сумма потоков, входящих в сток сети. Пример потока в транспортной сети:
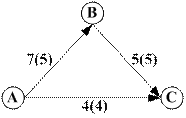
Для любой транспортной сети величина потока имеет максимальное значение, которое определяется теоремой Форда – Фалкерсона, которая утверждает, что величина максимального потока в сети равна величине минимального разреза, где разрезом транспортной сети называется такое множество дуг, удаление которых отделяет исток от стока. минимальным разрезом транспортной сети называется разрез с минимальной пропускной способностью. Пример. Транспортная сеть
имеет два разреза
|

 и
и  . Пропускная способность первого разреза равна 11 (7+4), а второго – 9 (4+5), поэтому максимальный поток в этой транспортной сети равен 9 = min(11, 9). Этот максимальный поток указан в круглых скобках.
. Пропускная способность первого разреза равна 11 (7+4), а второго – 9 (4+5), поэтому максимальный поток в этой транспортной сети равен 9 = min(11, 9). Этот максимальный поток указан в круглых скобках.


