Решение задач нелинейного программирования методом Лагранжа
Метод Лагранжа заключается в выполнении следующих действий. 1. Если в системе ограничений встречаются неравенства, то, вводя дополнительные переменные, преобразовать неравенства в равенства. 2. Для заданной системы ограничений и целевой функции составить функцию Лагранжа:
3. Приравнять к нулю все частные производные первого порядка функции L, и получить систему уравнений (в общем случае нелинейных уравнений):
4. Решить полученную систему и, тем самым, найти все стационарные точки 5. Исследовать каждую точку на наличие в ней экстремума функции если функция минимум, если все числа D1, D2, …, Dn являются положительными, максимум, если знаки чисел D1, D2, …, Dn чередуются, начиная с минуса, где
Если же числа Di не являются положительными или их знаки не чередуются, то вопрос о наличии экстремума функции в стационарной точке остаётся открытым и требует дополнительных исследований. Для решения задач нелинейного программирования целесообразно использовать программные системы символьных вычислений, например, систему MathCad. Пример. Решить методом Лагранжа в системе MathCad следующую задачу нелинейного программирования:
Решение. 1. Объявляем целевую функцию f и функцию Лагранжа L:
2. Находим стационарные точки: а) объявляем все частные производные первого порядка функции L:
б) приравниваем к нулю все частные производные первого порядка функции Лагранжа L и получаем систему, которую решаем с помощью блока Given:
Таким образом, функция f имеет одну стационарную точку (91, 89). 3. Для каждой стационарной точки проверяем наличие у функции f минимума или максимума. Для этого: а) объявляем все производные второго порядка целевой функции f:
б) вычисляем значения всех производных второго порядка функции f в каждой стационарной точке:
в) вычисляем значения членов последовательности
Так числа D1, D2 положительны, то функция f в точке (91, 89) имеет минимум, равный
Ответ. Функция
|

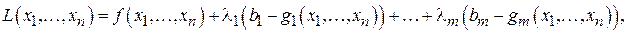 где
где 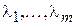 есть неопределённые коэффициенты[2].
есть неопределённые коэффициенты[2].
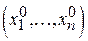 функции
функции 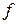 , то есть такие точки, в которых функция может иметь экстремумы (минимумы или максимумы).
, то есть такие точки, в которых функция может иметь экстремумы (минимумы или максимумы).

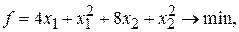
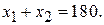

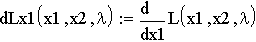

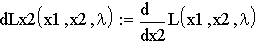
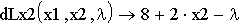

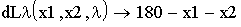


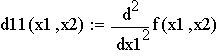
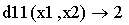

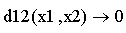


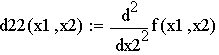


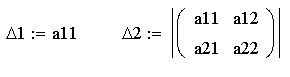

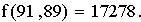
 при условии
при условии  имеет минимум 17278, который достигается при x1 = 91, x2 = 89.
имеет минимум 17278, который достигается при x1 = 91, x2 = 89.


