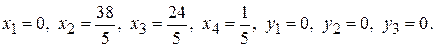Поиск опорного решения задачи линейного программирования
1. Преобразовать систему ограничений к стандартному виду:
Примечание. Переменные слева от равенств называются базисными, а в круглых скобках – свободные. 2. Если в системе (1) все ai ³ 0, то приравнять к нулю все свободные переменные и этим получить опорное решение. 3. Если в системе (1) найдётся ai < 0, то найти и поменять местами свободную переменную xk и базисную переменную xn (то есть свободную переменную xk ввести в состав базисных, а базисную переменную xn – в состав свободных). 4. Если обмен произвести удалось, то продолжить с п. 2, иначе опорного решения не существует. Пример. Найти опорное решение следующей задачи линейного программирования
Решение. 1. Приводим систему ограничений к стандартному виду: а) получаем систему линейных уравнений по правилу: если в системе ограничений есть неравенства, то в левые части неравенств со знаком "³" следует добавить новые переменные, а из левых части неравенств "£" – вычесть новые переменные: в системе ограничений (2) есть неравенства и все со знаком "£", поэтому, добавляем к левым частям неравенств новые переменные:
б) Приводим систему линейных уравнений (3) к ступенчатому виду: · записываем расширенную матрицу системы из коэффициентов при неизвестных и свободных членов:
· умножаем вторую строку на -1 и меняем местами первую и вторые строки:
· умножаем первую строку на 5 и складываем со второй, умножаем первую строку на 3 и складываем с третьей и получаем ступенчатый вид матрицы:
в) Приводим систему линейных уравнений к приведённому ступенчатому виду: · первую строку умножаем на -1, третью строку делим на -3:
· умножаем третью строку на -3 и складываем со второй, складываем третью и первую строки и получаем приведённый ступенчатый вид матрицы:
или
· приводим систему к стандартному виду:
Базисные переменные: x1, x2 и x3, свободные переменные: x4, y1, y2 и y3. 2. В системе (4) есть не отрицательные свободные члены, поэтому ищем для обмена свободную и базисную переменные: · взять любое уравнение с отрицательным свободным членом, в системе (4) берём первое уравнение; · если во взятом уравнении нет отрицательных коэффициентов при свободных переменных, то опорного решения не существует, в первом уравнении два отрицательных коэффициента при x4 и y3; · взять любую свободную переменную с отрицательным коэффициентом и выделить столбец, содержащий взятую переменную, возьмём переменную x4 и выделим столбец с x4;
· в выделенном столбце найти наименьшее отношение свободных членов к коэффициентам при свободных переменных, знаки которых совпадают со знаками свободных членов, в столбце с x4 два коэффициента в первой и второй строках, знаки которых совпадают со знаками свободных членов, находим минимальное отношение:
· взять базисную переменную, которая находится в строке с минимальным отношением, минимальное отношение находится в первой строке, поэтому берём базисную переменную x1:
(выделенные столбец и строка) · обменять местами выбранные свободную и базисную переменные, для этого: § выразить в выбранной строке свободную переменную через все оставшиеся и подставить полученное выражение во все оставшиеся уравнения в нашем случае меняем местами переменные x4 и x1: в первой строке выражаем x4 через оставшиеся переменные:
подставляем выражение для x4 во второе и третье уравнения:
и получаем новый стандартный вид системы:
В этой системе все свободные члены не отрицательные, поэтому, приравнивая к нулю все свободные переменные, получим опорное решение:
|

 (1)
(1) (2)
(2) (3)
(3)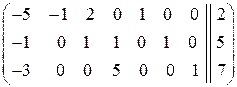 ;
; ;
;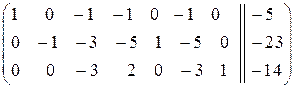 .
.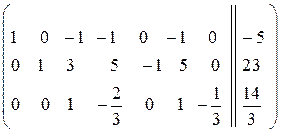 ;
;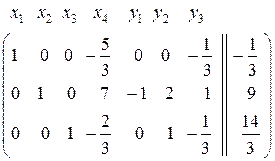 или
или 
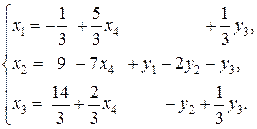
 (4)
(4)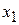
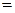
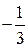
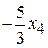
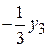
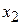


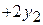

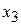

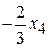
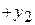
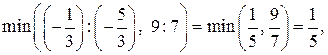
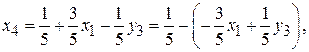
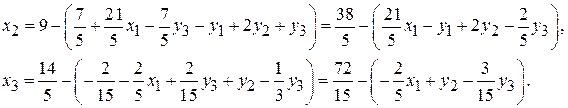
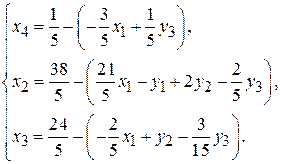 (5)
(5)