Линейное программирование
ГОУ ВПО РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИННОВАЦИОННЫХ ТЕХНОЛОГИЙ И ПРЕДПРИНИМАТЕЛСТВА ПЕНЗЕНСКИЙ ФИЛИАЛ
Ю.Ю. ГОРЮНОВ, Т.Ю. ГОРЮНОВА, Д.В. Дружинин
Теория и методы принятия решений
Учебное пособие
ПЕНЗА 2010
Теория и методы принятия решений (ТиМПР) – это наука, которая математическими методами обосновывает выбор одного из нескольких решений задачи (проблемы). Следует подчеркнуть, что окончательное решение принимает лицо ответственное за принятие решений, причём его выбор не всегда совпадает с рекомендуемым. Некоторые разделы ТиМПР: · математическое программирование (линейное программирование, нелинейное программирование, …); · динамическое программирование; · сетевое планирование; · потоки в сетях; · принятие решений в условиях неопределённости (теория игр). Для применения ТиМПР необходимо: 1) сформулировать задачу (проблему); 2) создать математическую модель (формализовать задачу в математической форме); 3) решить математическую модель, используя соответствующий раздел ТиМПР; 4) сформулировать предложения для принятия решения. Математическое программирование Линейное программирование Задача. Предприятие располагает тремя видами сырья, из которого изготавливает два вида продукции. Количество сырья, необходимого для производства каждого вида продукции, и доход от продажи единицы каждого вида приведены в следующей таблице:
Требуется составить план выпуска продукции, при котором доход от продажи был бы максимальным. Формализация (создание математической модели). Обозначим через x1 количество изготовленных изделий вида I, а через x2 – вида II. Тогда, учитывая имеющиеся запасы сырья, получим систему неравенств:
а доход от продажи составит Таким образом, для определения максимального дохода от продажи изделий необходимо найти максимальное значение функции Полученная математическая модель состоит из системы ограничений в виде системы линейных неравенств (1) и линейной целевой функции Задачи, в которых требуется найти максимальное (или минимальное) значение линейной целевой функции, при условии выполнения системы ограничений в виде системы линейных уравнений и/или неравенств, относятся к задачам линейного программирования.
|

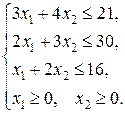 (1)
(1)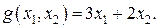
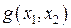 при условии выполнения системы неравенств (1) – это и есть математическая модель поставленной задачи.
при условии выполнения системы неравенств (1) – это и есть математическая модель поставленной задачи.


