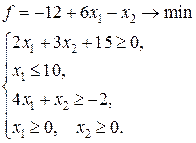Геометрическое решение задач линейного программирования
Если система ограничений и целевая функция задачи линейного программирования содержат две переменные, то эту задачу можно решить геометрически. Геометрическое решение задачи линейного программирования состоит в следующих действиях: 1) заменить в каждом ограничении знак неравенства на знак равно; 2) в прямоугольной системе построить соответствующие прямые, 3) выделить область точек на плоскости, координаты которых удовлетворяют системе ограничений (ограничению со знаком "³" удовлетворяют точки, находящиеся выше прямой, а знаку "£" – ниже прямой); 4) в целевой функции отбросить свободный член и построить соответствующую прямую; 5) при поиске максимума последнюю прямую параллельно перемещаем вверх, а минимума – вниз; 6) координаты точки области, которую прямая пересечёт последней, будут давать максимум (минимум) целевой функции, если эта точка существует. Пример. Решить задачу линейного программирования: f = x1 + 2x2 + 3 ® max
Решение. 1. Заменим в ограничениях знаки "£" на знак равно, получим уравнения двух прямых:
Построим эти прямые в прямоугольной системе координат:
2. Выделим область точек на плоскости, координаты которых удовлетворяют системе ограничений (на рисунке эта область 0ABC закрашена): первому ограничению удовлетворяют точки на плоскости, которые лежат ниже прямой L1, второму ограничению – ниже прямой L2, третьему – точки, находящиеся правее оси Ox2, четвёртому – выше оси Ox1 3. Отбросим свободный член в целевой функции, получим функцию y = x1 + 2x2, построим график этой функции (прямую L3). 4. Перемещая прямую L3 параллельно вверх, находим, что последней точкой области 0ABC, которую она пересечёт, будет точка B. 5. Для нахождения координат точки В решаем систему уравнений:
Вывод: максимальное значение целевой функции f равно 3 + 2*4 + 3 = 14 и достигается при x1 = 3, x2 =4. Примечание. Упражнения. Решить геометрически задачу линейного программирования, результат проверить в Microsoft Excel. 1. 3.
|


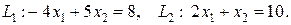

 решение системы: x1 = 3, x2 = 4.
решение системы: x1 = 3, x2 = 4. 2.
2. 
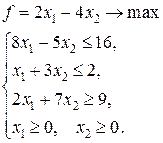 4.
4.