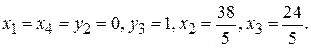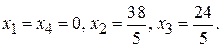Поиск оптимального решения
Если опорное решение найдено, то для отыскания оптимального опорного решения (минимального) необходимо: 1) представить целевую функцию из (5) получаем
2) если все коэффициенты в нашем случае есть положительный коэффициент; 3) если среди коэффициентов в целевой функции (6) положительный коэффициент только у свободной переменной y3, поэтому в системе (6) выделяем столбец с y3:
4) если в выделенном столбце нет положительных коэффициентов у свободных переменных, то целевая функция минимума не имеет, в выделенном столбце есть положительные коэффициенты; 5) в выделенном столбце найти положительный коэффициент, для которого отношение свободного члена (в той же строке) к этому коэффициенту является наименьшим для всех положительных коэффициентов выделенного столбца, в выделенном столбце только один положительный коэффициент, поэтому выделяем ту строку, в которой он находится, то есть первую строку:
6) свободную переменную в выделенном столбце ввести в состав базисных, а базисную переменную в выделенной строке ввести в состав базисных, свободную переменную y3 вводим в состав базисных, а базисную x4 – в состав свободных (выразить переменную y3 через все оставшиеся переменные в выделенной строке):
7) значение новой базисной переменной подставить во все оставшиеся уравнения и целевую функцию:
8) продолжить с п. 2). В целевой функции все коэффициенты являются отрицательными, поэтому Ответ. Минимум целевой функции равен -10 и достигается при
|

 в виде
в виде 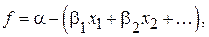 где все переменные x1, x2, … являются свободными,
где все переменные x1, x2, … являются свободными,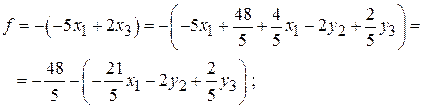 (6)
(6)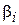 являются не положительными, то
являются не положительными, то 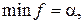
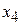
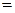
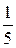
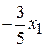
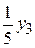
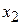
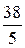
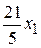

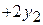
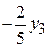
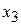

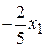
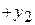
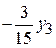
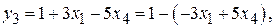
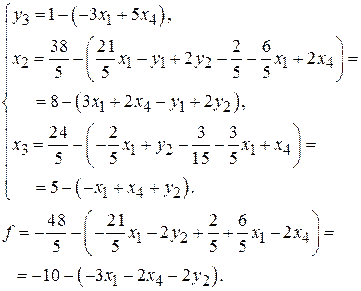
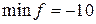 и достигается при (приравниваем к нулю свободные переменные)
и достигается при (приравниваем к нулю свободные переменные)