Динамическое программирование

Динамическое программирование представляет собой математический метод оптимизации решений при поэтапном (пошаговом) развитии ситуации, причём выбор оптимального решения зависит как от состояния ситуации на момент выбора очередного шага, так и от истории развития ситуации.

Следует подчеркнуть, что динамическое программирование применимо только для решения таких "многошаговых" задач, для которых справедливо утверждение: если за k шагов получено оптимальное решение, то выбор оптимального решения на k+1 шаге даёт оптимальное решение за все k+1 шагов.

Из сказанного вытекает, что при динамическом программировании оптимальное решение ищется "с конца", то есть от последнего к первому шагу.

Пример 1. Дана карта автомобильных дорог с нанесёнными расстояниями между населёнными пунктами

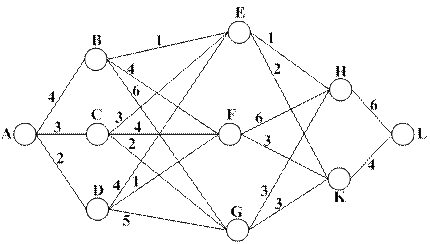
требуется найти наикратчайший маршрут между начальным пунктом A и конечным пунктом L.

Решение задачи методом динамического программирования (два этапа).

1. Двигаясь от конечного пункта L к начальному пункту A, помещаем в каждую вершину графа наикратчайшее расстояние от неё до конечной вершины L и отмечаем на карте соответствующую дорогу:

1)	расстояние от конечного пункта до него же равна 0.	2)		3)
4)		5)

Обратите внимание на то, что для нахождения наикратчайшего расстояния от очередного пункта до конечного достаточно среди всех соседних пунктов (в направлении конечного) найти такой, что бы сумма расстояний от очередного пункта до соседнего и от соседнего до конечного (она отмечается в вершине) была наименьшей.

2. Двигаясь от начального пункта A до конечного L по отмеченным дорогам,

находим наикратчайший маршрут ADFKL, длина которого равна 10.

Пример 2. Для производства некоторой продукции предприятие закупило новое оборудование. Зависимости производительности оборудования и затрат на его содержание и ремонт приведены в таблице:

	Время эксплуатации оборудования (лет)
Годовой выпуск продукции (тыс. руб)
Затраты на содержание и ремонт оборудования (тыс. руб)

Таблица 1.

Зная, что затраты на покупку нового оборудования составляют 40 тыс. рублей, а заменяемое оборудование списывается, составить план замены оборудования в течение 5 лет, при котором общая прибыль за данный период времени максимальна.

Решение. Вычитая из стоимости готовой продукции затраты на содержание и ремонт оборудования, получим зависимость прибыли предприятия от времени эксплуатации оборудования:

	Время эксплуатации оборудования (лет)
Прибыль (тыс. руб)

Таблица 2.

Примечание. Закупив в начале года новое оборудование, предприятие в этот год получает прибыль 80 – 40 – 20 = 20 (тыс. руб.).

В конце каждого года у предприятия есть выбор: оставить прежнее оборудование либо приобрести новое и получить прибыль согласно таблицы 2.

Отмечая вершинами графа концы финансовых лет, а весами рёбер прибыль от эксплуатации оборудования, получим:

что следует понимать следующим образом:

· в течение первого года (I) предприятие может получить прибыль только 20 тыс. руб.;

· в течение второго года (II) предприятие может получить прибыль 50 тыс. руб., если продолжит второй год эксплуатировать прежнее оборудование, либо 20 тыс. руб., если приобретёт новое;

· в течение третьего года (III) предприятие может получить прибыль 35 тыс. руб., если продолжит третий год эксплуатировать прежнее оборудование, либо 20 тыс. руб., если приобретёт новое, либо 50 тыс. руб., если второй год продолжит эксплуатировать оборудование, купленное во втором году, либо 20 тыс. руб., если в третий год купит новое оборудование.

Аналогично, понимаются веса рёбер в столбцах IV и V.

Примечание. В столбце V вместо двух рёбер из каждой вершины изображены по одной, которые соответствуют максимальным прибылям предприятия за пятый год. Например, эксплуатируя оборудование пять лет, предприятие получит прибыль 0 тыс. руб., что меньше прибыли 20 тыс. руб., если предприятие купит новое оборудование.

Двигаясь справа налево, пометим вершины максимальными прибылями предприятия за период, начиная от текущего года до пятого, а также отметим галочками соответствующие рёбра.

Таким образом, максимальная прибыль предприятия составит 175 тыс. руб.

Двигаясь справа налево по отмеченным рёбрам, определим, что максимальная прибыль будет получена, если предприятие сменит оборудование после двух лет его эксплуатации.