Лабораторная работа № 5
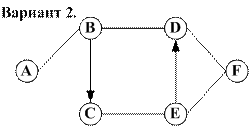
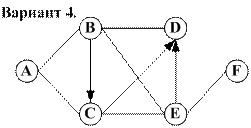
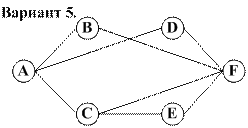
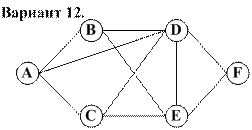
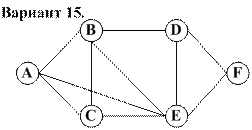
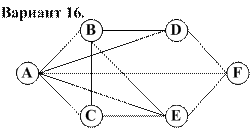
Задание. 1. Самостоятельно задать пропускные способности дуг и построить максимальный поток в транспортной сети. 2. Найти минимальный разрез сети и проверить справедливость теоремы Форда – Фалкерсона.
5. Принятие решений в условиях неопределённости Во многих сферах человеческой деятельности приходится принимать решения в ситуациях, в которых сталкиваются интересы двух или более враждующих (противоборствующих, конкурирующих, …) сторон, которые преследуют различные цели, причём результат любого действия каждой из сторон зависит от того, какое действие предпримет противник. Такие ситуации называются конфликтными. Примеры конфликтных ситуаций: · любая ситуация в ходе военных действий; · конкурентная борьба в экономике; · судопроизводство (обвинение и защита); · спортивные соревнования. Анализом конфликтных ситуаций занимается раздел математики под названием теория игр. Задача теории игр заключается в выработке рекомендаций по рациональному образу действий участников конфликта. Основные понятия теории игр · Игра – упрощённая модель конфликтной ситуации. · Игрок – сторона, участвующая в конфликте. · Парная игра – игра, в которой сталкиваются интересы двух сторон. · Игра с нулевой суммой – парная игра, в которой выигрыш одной стороны равен проигрышу другой. · Ход – выбор допустимого действия и его осуществление. · Личный ход – сознательный выбор игроком допустимого действия и его осуществление. · Случайный ход – выбор допустимого действия с помощью механизма случайного выбора (например, подбрасывания монеты) и его осуществление. · Правила игры – совокупность условий, регламентирующая: Ö возможные действия игроков, Ö объём сведений каждой стороны о поведении другой, Ö результат, к которому приводит каждая совокупность ходов. · Стратегия – совокупность правил, определяющая выбор варианта действий при каждом ходе игрока в зависимости от ситуации, сложившийся в игре. · Оптимальная стратегия – стратегия, которая при многократном повторении игры обеспечивает игроку максимальный средний выигрыш[5]. · Конечная игра – у каждого игрока имеется конечное количество стратегий. · m ´ n игра – конечная парная игра, в которой у одного игрока имеется m стратегий, а у второго n стратегий. Основное предположение теории игр. Противник так же как разумен, как и мы сами, и делает всё для того, чтобы помешать нам добиться максимального среднего выигрыша. 5.2. Платёжная матрица игры Платёжной матрицей m ´ n игры с нулевой суммой (или, просто, матрицей игры) называется матрица
в которой A1, …, Am – все стратегии игрока A, B1, …, Bm – все стратегии игрока B, aij – выигрыш (положительный или отрицательный) игрока A при выборе им стратегии Ai и стратегии Bj игроком B. Пример. Игра "поиск". Игрок A прячется в одном из двух убежищ, а игрок B его ищет. Правила игры: если игрок B находит A, то A платит ему 1 рубль, в противном случае игрок B платит A 1 рубль. Стратегии игроков: игрок A: A1 – спрятаться в убежище № 1, A2 – спрятаться в убежище № 2; игрок B: B1 – искать в убежище № 1, B2 – искать в убежище № 2; Матрица игры "поиск":
Некоторые выводы, вытекающие из игры "поиск". Если игра проводится один раз, то говорить о преимуществе той или иной стратегии смысла нет. Если при многократном проведении игры игрок будет придерживаться одной стратегии или чередования стратегий в определённой последовательности, то противник догадается об этом и начнёт выигрывать. Поэтому от верного проигрыша игроков может спасти только случайное чередование стратегий. Например, игрок перед своим ходом подбрасывает монету и, если выпала "решка", то игрок выбирает первую стратегию, а если "орёл", то вторую.
|