Решение игр в смешанных стратегиях
Если парная игра не имеет седловой точки, то она не имеет и решения, то есть, делая личные ходы (или, говоря иначе, в чистых стратегиях), игрок A гарантирует себе выигрыш, равный нижней цене игры, которая, вообще говоря, меньше верхней цены игры. Если же игрок A будет чередовать свои стратегии случайным образом или, говоря иначе, придерживаться смешанной стратегии, то он получит оптимальную стратегию, которая в некоторых случаях будет гарантировать ему бόльший выигрыш. Определение. Пусть игрок A имеет m стратегий, а игрок B – n стратегий. Смешанной стратегией игрока A называется набор вероятностей SA = (p1, p2, …, pm), где p1 + p2 +… + pm = 1, с которыми он чередует свои стратегии. Аналогично определяется смешанная стратегия игрока B как набор SB = (q1, q2, …, qm), где q1 + q2 +… + qn = 1. Имеет место следующая теорема. Теорема (основная теорема теории игр). Любая m ´ n игра имеет решение в смешанных стратегиях и её решение может получено методами линейного программирования. Доказательство. Пусть m ´ n игра имеет матрицу
требуется найти решение игры, то есть две оптимальные смешанные стратегии игроков SA = (p1, p2, …, pm) и SB = (q1, q2, …, qm), где p1 + p2 +… + pm = 1 и q1 + q2 +… + qn = 1. Во-первых, можно считать, что цена игры n (пока неизвестная) больше нуля. Действительно, если n £ 0, то это означает, что некоторые элементы матрицы игры не положительные. Тогда найдём число M > 0, которое прибавим ко всем элементам матрицы игры и получим новую матрицу с положительными элементами. Это сложение сделает новую цену игры n + M положительной, но не изменит решения игры. Во-вторых, предположим, что игрок A применяет свою оптимальную смешанную стратегию
Стратегия
Разделим обе части всех неравенств на положительное число n и обозначим
тогда система ограничений примет вид
Далее, так как p1 + p2 +… + pm = 1, то
Игрок A стремится максимизировать свой средний выигрыш n, то есть минимизировать отношение Таким образом, получаем задачу линейного программирования:
Заметим, что эта задача имеет решение, найдя которое Аналогичные рассуждения дают оптимальную стратегию обозначим
тогда оптимальная стратегия
причём Применим основную теорему теории игр для отыскания оптимальных стратегий игроков в игре "поиск". 1. Матрица игры "поиск"
2. Для нахождения оптимальной стратегии
Так как последняя система ограничений эквивалентна системе
то минимум функции Так как Итак, чередуя свои обе стратегии с вероятностями Аналогичные рассуждения приводят к тому, что игрок B, чередуя свои стратегии с вероятностями
|


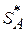 , а игрок B свою чистую стратегию Bj. В этом случае средний выигрыш игрока A будет равен
, а игрок B свою чистую стратегию Bj. В этом случае средний выигрыш игрока A будет равен

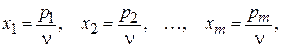


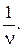
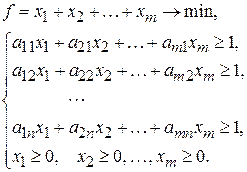
 найдём новую цену игры
найдём новую цену игры 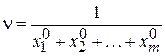 , вычтя из которой число M, получим искомую цену игры.
, вычтя из которой число M, получим искомую цену игры. игрока B:
игрока B: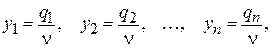
 игрока B есть решение следующей задачи линейного программирования:
игрока B есть решение следующей задачи линейного программирования:

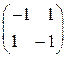 содержит отрицательные элементы, поэтому, прибавляя к её элементам число M= 1, получим
содержит отрицательные элементы, поэтому, прибавляя к её элементам число M= 1, получим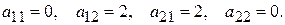
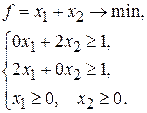
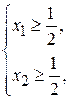
 равен 1 и достигается при
равен 1 и достигается при 
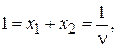 то n = 1. Вычитая из n число M = 1, получим, что цена игры равна 0 = 1 – 1, а оптимальная стратегия
то n = 1. Вычитая из n число M = 1, получим, что цена игры равна 0 = 1 – 1, а оптимальная стратегия 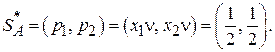
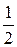 , игрок A гарантирует себе средний выигрыш, равный 0, что больше нижней цены игры -1 при чистых стратегиях.
, игрок A гарантирует себе средний выигрыш, равный 0, что больше нижней цены игры -1 при чистых стратегиях.


