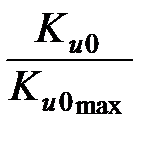Количественные характеристики различных типов одноконтурных входных цепей могут быть получены из рассмотрения обобщенной эквивалентной схемы (рис. 1.2). В этой схеме комплексное сопротивление связи антенны с контуром Z св = r св + j x свотнесено к антенной цепи. Тогда полное комплексное сопротивление всей антенной цепи
 , (1.1)
, (1.1)
где  ;
;  ;
;  и
и  – активные составляющие: наводимой во входной цепи эдс, комплексного сопротивления связи антенны с контуром соответственно;
– активные составляющие: наводимой во входной цепи эдс, комплексного сопротивления связи антенны с контуром соответственно; 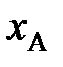 и
и  – реактивные составляющие: наводимой во входной цепи эдс, комплексного сопротивления связи антенны с контуром соответственно.
– реактивные составляющие: наводимой во входной цепи эдс, комплексного сопротивления связи антенны с контуром соответственно.
Полная выходная проводимость антенной цепи
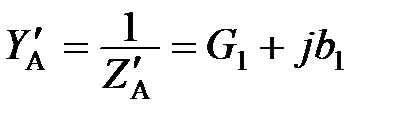 , (1.2)
, (1.2)
где  ;
; 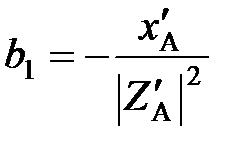 .
.
На рис. 1.2 антенная цепь представлена генератором тока  и выходной проводимостью
и выходной проводимостью 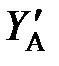 .
.
Рис. 1.2. Обобщенная эквивалентная схема входной цепи
Антенная цепь подключается к избирательной системе (контуру) через коэффициент включения p 1 = U 1/ U к, (где U 1 и U к – напряжения на входе контура и на конденсаторе C к соответственно), характеризующий степень связи антенной цепи с контуром. Электронный прибор усилителя радиосигналов, подключенный к выходу контура, обладает входной проводимостью:
Y вх = G 2 + jb 2, (1.3)
где G 2– активная, а b 2= ω C 2реактивная (емкостная) составляющие электронного прибора. Этот прибор подключается к контуру через коэффициент включения p 2 = U вых/ U к.
При настройке входной цепи на частоту ωснеобходимо учитывать, что резонансная частота контура ω0определяется не только значениями индуктивности L к и емкости C к, а также в равной степени внешними по отношению к контуру реактивными проводимостями b 1 и b 2. Таким образом, эквивалентная емкость контура

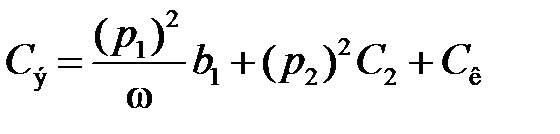 . (1.4)
. (1.4)
Аналогичной зависимостью будет определяться и эквивалентная проводимость G эконтура:
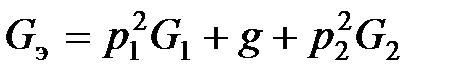 . (1.5)
. (1.5)
Таким образом, схему на рис. 1.2 удобно заменить более простой эквивалентной схемой рис. 1.3.
Рис. 1.3. Эквивалентная схема входной цепи
На этом рисунке
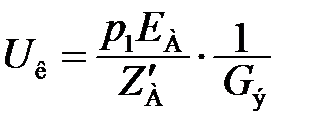 , (1.6)
, (1.6)
U вых = p 2 U к. (1.7)
Резонансный коэффициент передачи
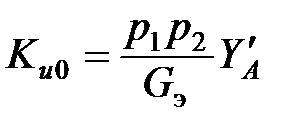 . (1.8)
. (1.8)
Резонансный коэффициент передачи входной цепи Ku 0 при заданных параметрах антенной цепи, контура и электронного прибора зависит от коэффициентов включения p 1и p 2, которые являются вещественными и могут изменяться в пределах: 0 £ p 1 £ 1 и 0 £ p 2 £ 1. Коэффициент передачи в данных условиях определяется этими двумя переменными и, следовательно, его максимум может быть найден при совместном решении следующих двух уравнений:
 ;
;  . (1.9)
. (1.9)
Можно показать, что Ku 0 будет иметь максимум при G 1 ³ G 2 + g, когда p 2 = 1 и
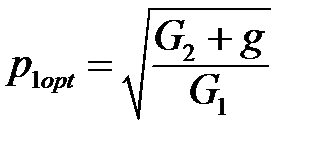 , (1.10)
, (1.10)
G 2 ³ G 1 + g, когда p 1 = 1 и  . (1.11)
. (1.11)
Активная составляющая проводимости антенной цепи G 1, как правило, значительно больше входной проводимости G 2в случае использования в качестве электронного прибора транзисторов или интегральных микросхем. Поэтому при выполнении условия (1.10) обычно достигается максимальное значение резонансного коэффициента передачи.
Учитывая (1.2) и подставляя (1.10) в (1.8), получаем
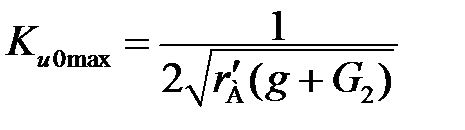 . (1.12)
. (1.12)
Полагая, что рассматриваемый контур является трансформатором сопротивлений, легко видеть, что, согласно (1.10),
 . (1.13)
. (1.13)
Это выражение является условием передачи максимальной мощности от генератора к нагрузке. Следовательно, подбор оптимального значения коэффициента p 1соответствует согласованию нагрузочной проводимости с кажущейся выходной проводимостью генератора тока.
Рассмотрим отношение резонансных коэффициентов передачи по напряжению:  . Согласно (1.8) и (1.12) имеем
. Согласно (1.8) и (1.12) имеем
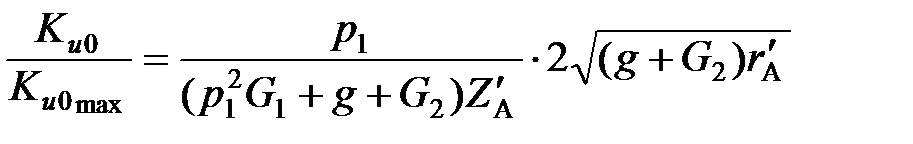 . (1.14)
. (1.14)
Обозначим p 1/ p 1 opt = а. Принимая во внимание, что 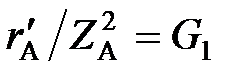 , и учитывая (1.10), получаем
, и учитывая (1.10), получаем
 . (1.15)
. (1.15)
Для режима передачи максимальной мощности от генератора к нагрузке оптимальная величина эквивалентной проводимости контура входной цепи, с учетом (1.10), определяется выражением
 . (1.16)
. (1.16)
Отношение 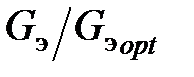 будет иметь вид
будет иметь вид
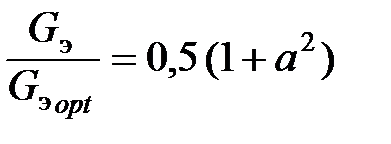 . (1.17)
. (1.17)
графики, иллюстрирующие зависимости (1.15) и (1.17), приведены на рис. 1.4. Из этих кривых видно, что в случае оптимальной связи антенны с контуром полоса пропускания входной цепи, пропорциональная G э возрастает более чем в два раза по отношению к полосе пропускания ненагруженного контура. Увеличение связи выше оптимальной приводит к существенному увеличению полосы пропускания. Наоборот, при связи в два раза меньше оптимальной (а = 0,5) полоса пропускания всего на 25 % превышает полосу пропускания ненагруженного контура. Дальнейшее уменьшение связи практически незначительно улучшает избирательность входной цепи.
Рис. 1.4. Зависимости отношений  и и  от величины от величины 
|
Следовательно, для обеспечения высокой избирательности и большого коэффициента передачи выбирают коэффициент a близким к значению 0.5, так как при этом коэффициент передачи составляет 80 % от максимального, а избирательность входной цепи мало отличается от избирательности ненагруженного контура.

 , (1.1)
, (1.1) ;
;  ;
;  и
и  – активные составляющие: наводимой во входной цепи эдс, комплексного сопротивления связи антенны с контуром соответственно;
– активные составляющие: наводимой во входной цепи эдс, комплексного сопротивления связи антенны с контуром соответственно; 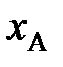 и
и  – реактивные составляющие: наводимой во входной цепи эдс, комплексного сопротивления связи антенны с контуром соответственно.
– реактивные составляющие: наводимой во входной цепи эдс, комплексного сопротивления связи антенны с контуром соответственно.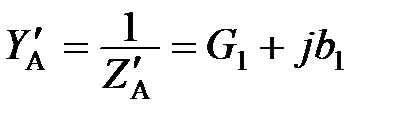 , (1.2)
, (1.2) ;
; 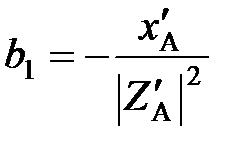 .
. и выходной проводимостью
и выходной проводимостью 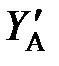 .
.
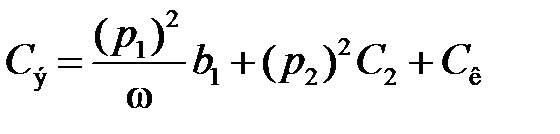 . (1.4)
. (1.4)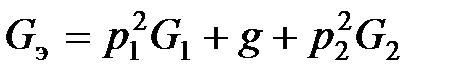 . (1.5)
. (1.5)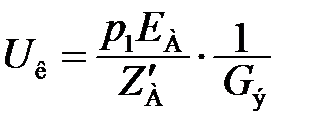 , (1.6)
, (1.6)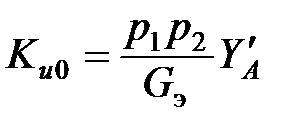 . (1.8)
. (1.8) ;
;  . (1.9)
. (1.9)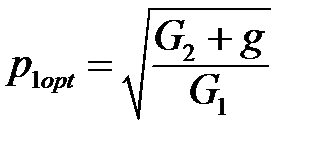 , (1.10)
, (1.10) . (1.11)
. (1.11)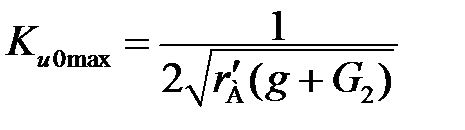 . (1.12)
. (1.12) . (1.13)
. (1.13) . Согласно (1.8) и (1.12) имеем
. Согласно (1.8) и (1.12) имеем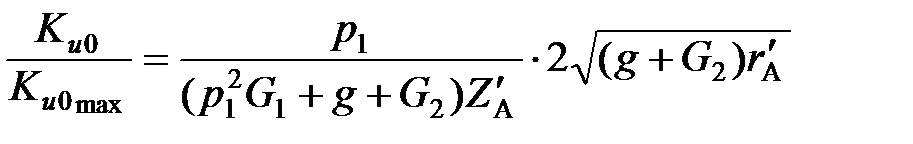 . (1.14)
. (1.14)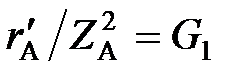 , и учитывая (1.10), получаем
, и учитывая (1.10), получаем . (1.15)
. (1.15) . (1.16)
. (1.16)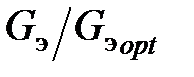 будет иметь вид
будет иметь вид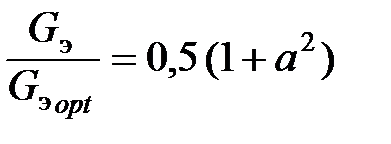 . (1.17)
. (1.17) и
и  от величины
от величины