Расчет выборки
Количество членов выборочной совокупности, или иначе говоря, объем выборки можно определить по следующей формуле:
где n – объем выборки; sх – средняя квадратическая ошибка; t – отношение «максимальной» ошибки к средней квадратической ошибке, устанавливаемой в зависимости от требуемой степени достоверности и в предположении, что действительная ошибки не превзойдет максимальную; m(дон.) – допустимая ошибка выборки (выражается в процентах).
Средняя квадратическая ошибка вычисляется по формуле
где n – число обследованных лиц; ∑ - знак суммирования.
Показатель m(дон.) выражается в процентах; он может принимать значения 1,2,3,4 и 5%. Больше 5% допускать ошибку нежелательно. Значение t зависит от вероятности того, что действительная ошибка не превышает допустимую. Так, при вероятности Р = 0,997 t = 3. При вероятности Р = 0,994 t = 2.
Если ошибка не должна превышать 2%, то объем выборки
Необходимое количество наблюдений (объем выборки) изменяется обратно пропорционально квадрату допустимой ошибки, прямо пропорционально дисперсии признака и надежности заключения выражаемого t. Приведенная формула применима собственно к случайной повторной выборке. Для бесповторной выборки формулы будут иными. Кроме того, эта формула применяется в том случае, если мы раньше изучали это признак и нам известны его средняя арифметическая ( Если же эти данные неизвестны, т.е. мы впервые принимаемся за изучение признака, то можно воспользоваться формулой для определения его доли:
где
В том случае, если неизвестны p и q, берут из наибольшее значение: p=0,5 и q=0,5. Тогда pq=0,25. Этим обеспечивается большая надежность результатов. Приведенные формулы применимы для однородных выборок. Они даны лишь в качестве примеров. Существуют и другие методы расчета выборки, хотя математический аппарат достаточно однороден во всех случаях.
Другая задача – как отобрать людей для обследования? В практике социологических исследований обычно используются следующие типы выборок. Случайная выборка заключается в том, что каждый член генеральной совокупности имеет шанс попасть в выборку. Техника отбора бывает повторной и бесповторной. В урну закладываются номера членов генеральной совокупности, из них выбирается столько номеров, сколько составляют выборку. Номера идентифицированы с фамилиями людей. Бесповторная случайная выборка заключается в том, что номер в урну не возвращается. Если номера возвращают в урну (если повторно попадает тот же номер его снова возвращают), выборка называется повторной случайной выборкой. Другой метод отбора – систематический. Он заключается в том, что исследователь берет алфавитный список, например, список избирателей, определяет шаг и затем отбирает фамилии тех лиц, которые будут обследованы. Например, из списка, насчитывающего 3000 фамилий, нам надо отобрать 300 человек, т.е. шаг равен 10. Берем в списке 5-ю фамилию, затем 15-ю, 25-ю и так до конца. В итоге мы отберем 300 человек для обследования. Типическая (стратифицированная, районированная) выборка позволяет увеличить репрезентативность и точность исследования. Она заключается в том, что, например, предприятия распределяются по некоторым типам. Можно выделить крупные, средние и мелкие предприятия и случайно выбирать единицы из этих трех генеральных совокупностей. Серийная (гнездовая) выборка заключается в следующем. Случайным образом отбираем, например, учебные группы в вузе, а в группе опрашиваем каждого. Обычно исследователи используют серийную, гнездовую выборку в том случае, когда проводят опросы рабочих по месту их работы.
(Схема выборка) – Генеральная совокупность (Выборочная совокупность) → минимальное число наблюдений → минимальная ошибка → равные шансы попасть в выборку → точность измерения.
Виды выборок: пропорциональная (непропорциональная); многоступенчатая; многофазная; монографическое обследование; случайная (повторная и бесповторная); типическая (районированная); серийная (гнездовая); интервальная (систематическая); квотный отбор.
Случайная, стратифицированная, серийная выборки относятся к выборкам, построенным на принципе случайного отбора. Тем самым каждому члену выборочной совокупности обеспечивается определенный (а иногда и равный) шанс быть отобранным, что необходимо для оценки выборочных ошибок.
На иной основе базируется отбор по квотам. Так, после того как принято решение относительно распределения выборки (например, сколько должно быть мужчин и женщин в каждой возрастной группе и в каждом социальном слое) и интервьюеру дано задание опросить запланированное число единиц в квоте, фактический выбор единиц, включаемых в выборку, падает на интервьюеров. Поэтому выборка в пределах квот не является случайной. Квоты же определяются на основе стратификации. Например, сначала выделяются типы по полу, возрасту, социальному положению, а затем идет отбор по квотам.
В случае территориальных выборок применяется также интервальный отбор. Так, город можно разделить на типы районов (страты) или на участки, из которых извлекается случайная выборка. Затем по определенному интервалу отбираются улицы и дома. Например, каждая 2-я улица и каждый 20-й дом на улице. Это случайный своеобразный отбор. В качестве основы выборки вместо списков используются карты районов, участков города. Интервальный отбор можно рассматривать и как разновидность серийного, ибо дома, например, можно рассматривать как серии. Обычно в практике социологических исследований приходится формировать многоступенчатый отбор. При этом изучаемый материал состоит из некоторого числа единиц отбора первой ступени, каждая из которых в свою очередь состоит из единиц второй ступени и т.д. В социологических обследованиях также встречается многофазный отбор. Он сводится к тому, что одни данные собираются на основании изучения всех единиц выборки, другие – только некоторых из них. Последние составляют подвыборку из единиц первоначальной выборки. Часто в социологии применяется монографическое обследование как разновидность несплошного наблюдения. Оно сводится к детальному изучению либо одной, отдельно взятой единицы (деревня, город, завод, колхоз и т.д.), либо части объекта. При формировании выборочный совокупностей следует добиваться полноты, точности, адекватности, удобства, репрезентативности.
|

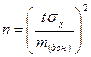 ,
, ,
,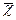 - средняя арифметическая признака в изучаемой совокупности;
- средняя арифметическая признака в изучаемой совокупности;
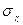 ).
).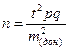 ;
;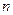 - объем выборки;
- объем выборки; и
и 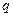 - вероятности появления признака в выборке;
- вероятности появления признака в выборке;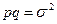 - средняя квадратическая ошибка для альтернативных признаков.
- средняя квадратическая ошибка для альтернативных признаков.


