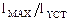МОДЕЛИРОВАНИЕ И ОПТИМИЗАЦИЯ ЭЛЕКТРОМЕХАНИЧЕСКОЙ СИСТЕМЫ ПРИВОДА ПРОКАТНЫХ ВАЛКОВ
Цель работы: построить модель электромеханической системы привода прокатных валков и оптимизировать настройки регулятора.
Теоретическая часть Электромеханическая система привода прокатных валков может быть разделена на механическую и электрическую подсистемы. Механическая подсистема (рис. 1) включает ротор электродвигателя 1, соединенный промежуточным валом 2 с редуктором 3, выходной вал которого соединен с шестеренной клетью 4. Выходные валы шестеренной клети соединены шпинделями 5 с верхними и нижними рабочими валками 6. В клетях кватро, кроме того, имеются опорные валки 7, фрикционно связанные с рабочими валками.
Рис. 1. Схема механической подсистемы привода валков прокатной клети
Электрическая подсистема привода включает прокатный двигатель, обычно - постоянного тока с независимым возбуждением. На рис. 2 показаны его обмотки ротора 1 и статора 2. С валом ротора механически связан тахогенератор 4 - датчик обратной связи системы автоматической стабилизации скорости (САРС) прокатного двигателя. В регулятор 7 системы поступают сигналы обратной связи по скорости и по току якорной цепи - от датчика тока 5. САРС обычно строится как система подчиненного регулирования с внутренним контуром тока и внешним током скорости. Выходной сигнал регулятора 7 управляет выходным напряжением многофазного управляемого выпрямителя 6, которое питает якорную цепь. При работе двигателя на скоростях выше основной регулятор 7 воздействует дополнительно на управляемый выпрямитель 3 возбуждения, уменьшая напряжение на обмотке статора 2, и, следовательно, поток возбуждения. Как правило, собственные частоты механической подсистемы выше, чем частота среза электрической подсистемы. Тогда их взаимное влияние не проявляется, и эти подсистемы можно моделировать отдельно. Однако, если промежуточный вал 2 имеет большую длину, то низшая собственная частота механической подсистемы уменьшается до значений, близких к частоте среза электрической подсистемы, и наблюдается взаимное влияние подсистем.
Рис. 2. Схема электрической подсистемы привода валков прокатной клети
Во многих случаях для описания динамических процессов в механической подсистеме можно применить двухмассовую вращательную расчетную систему (рис. 3), где вращающейся массе 1 соответствует ротор электродвигателя, а вращающаяся масса 2 соответствует сумме остальных вращающихся масс, приведенных к входному валу редуктора.
Рис. 3. Двухмассовая вращательная система где q1 - момент инерции электродвигателя; q2 - момент инерции шестерен редуктора, шестеренной клети и валков, приведенный по входному валу редуктора; c12 - жесткость валопровода между электродвигателем и редуктором; M1 - вращающий момент электродвигателя; M2 - момент усилия прокатки, приведенный ко входному валу редуктора; M12 - момент сил упругости в валопроводе между электродвигателем и редуктором.
Приведение масс производится исходя из условия сохранения кинетической энергии системы. Если q - момент инерции приводимой массы, w’ - ее угловая скорость, а w - угловая скорость звена приведения, то приведенная масса
где i - передаточное отношение зубчатой или фрикционной передачи:
где d1, d2 - диаметры соответственно входного и выходного валов при фрикционной связи; z1, z2 - числа зубьев соответственно входной и выходной шестерен для зубчатого зацепления. Момент инерции роторов электродвигателей берут из справочников. Момент инерции сплошного цилиндрического тела вращения (валок, вал, шестерня) диаметром dc и массой m определяется по формуле:
Приведение моментов сил, приложенных к вращающимся массам, нужно выполнить одновременно с приведением масс. Оно производится из условия равенства работ приводимого и приведенного момента силы. Если к приводимой массе приложен момент силы M’, а передаточное отношение к валу приведения равно i, то приведенный момент силы будет
Приведение жесткостей валопроводов, соединяющих приводимые массы (например, жесткостей шпинделей между шестеренной клетью и валками) осуществляется из условия равенства потенциальных энергий закрученных валов. Если приводимая жесткость равна c’, то приведенная жесткость
Жесткость цилиндрического вала определяется по формуле:
где G - модуль сдвига, d, L - соответственно диаметр и длина вала. Приведение массы вала к концевым массам осуществляется из условия равенства полной кинетической энергии крутильной системы до и после приведения вала. В первом приближении можно пользоваться следующим правилом: 1. Приведенный момент инерции вала равен 1/3 его момента инерции. 2. Этот приведенный момент делится на две части, пропорциональные моментам инерции граничных масс и добавляется к их моментам инерции. Таким образом можно определить параметры расчетной системы (рис. 3).
Математическая модель системы Уравнения равновесия моментов сил в механической системе:
где Dj1, Dj2 - приращения углов закручивания вала возле масс q1 и q2. Дважды продифференцировав (9), получим
Найдем
Здесь коэффициент демпфирования обычно» 0.1. В отличие от уравнения для M12 в форме (5.9), уравнение в форме (11) исключает накопление ошибок при вычислении малых разностей углов закручивания валопровода (Dj1 - Dj2). Таким образом, уравнения (7), (8), (11) образуют математическую модель механической вращательной системы привода валков. Уравнения электрической системы: - вращающий момент: M1 = (kM · Ф) · I (12) где (kM · Ф) - коэффициент вращающего момента при постоянном потоке возбуждения Ф= const; I - величина тока в якорной цепи. - напряжение в якорной цепи:
где R - сопротивление якорной цепи, L - индуктивность якорной цепи. Уравнение регулятора (в операторной форме)
В простейшем случае обратная связь по величине тока якорной цепи отсутствует, т.е. W2(p) = 0, а регулятор скорости можно выбрать пропорционально-интегральным.
Порядок выполнения работы
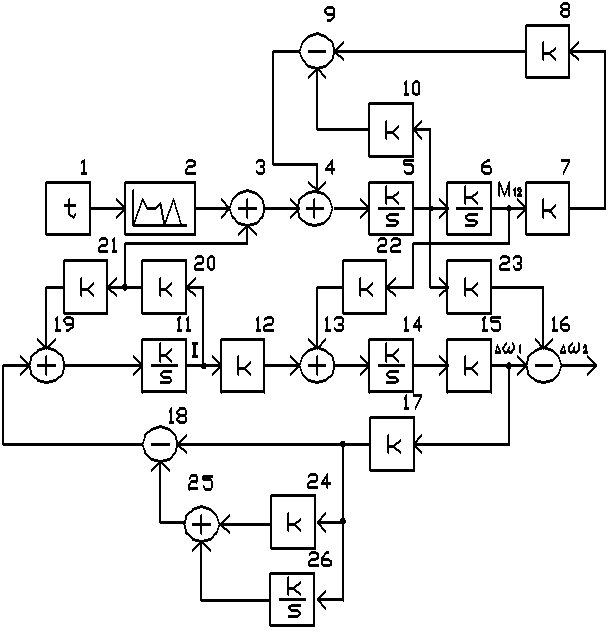
1. Набрать схему модели электромеханической системы привода прокатных валков (рис. 4) в пакете и подставить коэффициенты в соответствии с заданным вариантом. В блоке 2 установить значения момента прокатки M2 и времени захвата полосы валками tз (табл. 1), соответствующие закону изменения M2 при захвате (рис. 5). Все остальные значения по базовому режиму: k5 = 1, k6 = 10, k7 = -1, k8 = 5.46, k10 = 0.5, k11 = -1, k12 = -0.278, k14 = 1, k15 = -1, k17 = 0,755, k20 = 0.1, k21 = 23.8, k22 = 1.07, k23 = 1.64.
Рис. 4. Схема модели электромеханической системы
Рис. 5. Закон изменения момента прокатки при захвате.
Табл. 1
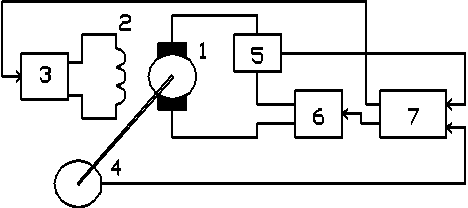
2. Получить графики изменения переменных Dw1, Dw2, M12, I без регулятора. Для этого необходимо установить kр = k24 = 0 и k26 = 1/Tи = 0. 3. Включить в схему регулятор. Методами половинного деления и координатного спуска подобрать параметры ПИ-регулятора таким образом, чтобы: a) целевая функция (длительность переходного процесса (ДПП) Dw1) была минимальной; b) соблюдались следующие ограничения: - максимальная величина момента M12 не должна превышать установившуюся величину более чем в 4 раза; - максимальная величина тока не должна превышать установившуюся величину более чем в 1,5 раза. При подборе параметров сначала принять Tи = ¥ (k26 = 0) и методом половинного деления найти оптимальное значение kр. Далее поддерживая kр= const, таким же образом подобрать Tи. Затем снова принять Tи= const и подобрать kр. Цикл повторяется до получения оптимальных значений настроек регулятора. 4. Данные экспериментов занести в табл. 2. Табл. 2
5. После получения оптимальных значений параметров регулятора зарисовать графики Dw1, Dw2, M12, I. 6. Сделать выводы по работе, раскрыв ответы на контрольные вопросы.
Контрольные вопросы 1. От чего зависят максимальная и установившаяся величины нагрузки в связи? 2. От чего возникают «биения» в переходном колебательном процессе? 3. Связаны ли переходные процессы в электрической и механической подсистемах? 4. Как можно добиться дальнейшего увеличения коэффициентов динамичности в исследуемой системе?
|



 (1)
(1) (2)
(2)
 (3)
(3) (4)
(4) (5)
(5)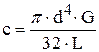 (6)
(6) (7)
(7) (8)
(8) (9)
(9)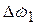 ,
, 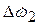 - угловые ускорения сосредоточенных масс (моментов инерции) q1 и q2;
- угловые ускорения сосредоточенных масс (моментов инерции) q1 и q2;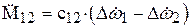 (10)
(10) (11)
(11) (13)
(13) (14)
(14)