Уравнение состояния

Параметры p, V, T связаны между собой функциональной зависимостью f (p, V, T) = 0, которая называется характеристическим уравнением состояния рабочего тела. Характеристическое уравнение состояния имеет большое значение в термодинамике. Это уравнение позволяет определить один из параметров состояния по известным двум другим.

Для большинства реальных рабочих тел аналитическая зависимость между параметрами состояния достаточно сложна и воспользоваться ею для определения параметров состояния в ряде случаев бывает затруднительно.

Наиболее простое уравнение состояния может быть получено для идеального газа, под которым будем понимать газ, в котором отсутствуют силы межмолекулярного взаимодействия и объём молекул исчезающе мал по сравнению с объемом газа. При этом молекулы представляют собой материальные точки.

Заметим, что зачастую реальные газы ведут себя как идеальные.

Характеристическое уравнение состояния идеального газа может быть представлено в виде:

.

В приведенных уравнениях:

р – абсолютное давление, Н/м²;

V – полный объем газа, м³;

M – масса газа, кг;

T – абсолютная температура, К;

R – газовая постоянная, Дж/кг×К, зависящая от природы газа.

Приведенное выше уравнение может быть записано для 1 моля газа, которое называют уравнением Клайперона-Менделеева:

.

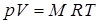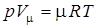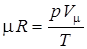Величина является постоянной для 1 кмоля любого газа во всех состояниях и называется поэтому универсальной газовой постоянной. Универсальная газовая постоянная может быть легко вычислена при нормальных физических условиях:

.

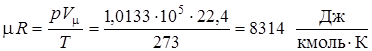Газовая постоянная для газа может быть вычислена по формуле:

,

где μ – молекулярная масса.