Статистический смысл II начала термодинамики
Состояние макросистемы может быть охарактеризовано параметрами p, V, T, ν и др. В этом случае говорят, что задано макросостояние. Можно также задать состояние макросистемы более детально, через характеристики всех молекул (их скорости, энергии, координаты), тогда такое детальное описание называют микросостоянием. Любое макросостояние системы может быть реализовано различными способами, или микросостояниями. Число различных микросостояний, соответствующих данному макросостоянию, называется статистическим весом макросостояния. В качестве примера рассмотрим способы, которыми могут распределяться N = 4 молекулы с номерами №1, 2, 3, 4 между двумя половинами сосуда с газом без учета распределения Максвелла по скоростям, рис.. Вероятность того, что любая из молекул может находиться в половине А равна, очевидно, 1/2. Вероятность одновременного пребывания одной и другой молекул 1/2·1/2 = 1/22 как вероятность независимых событий, для трех молекул - 1/23, четырех – 1/24. Вероятность любого размещения 4-х молекул также равна 1/24. Каждое размещение это микросостояние системы и вероятность каждого из них одинакова и равна 1/24. Все возможные распределения 4-х
А В

Рис.
Как видно из таблицы, всего микросостояний – 16 = 24 =2N. Под макросостоянием в данном случае будем понимать состояние, при котором в половине А сосуда: находится, например одна молекула (любая), а в половине В – три любые молекулы. Такие состояния реализуется 4-мя способами. Статистический вес данного макросостояния равен 4, а вероятность 4/16. Макросостояние с 2-мя молекулами в каждой из половин, реализуется с помощью 6 микросостояний и его статистический вес Ω=6, а вероятность этого макростояния максимальна. Предположим, что вначале все молекулы находились в половине А сосуда, затем некоторые из молекул, двигаясь беспорядочно, перейдут в В, это означает, что «газ» расширился. Далее макросостояние системы будет меняться случайным образом, но чаще будет реализоваться то из них, которому соответствует максимальное Ω, т.е. более вероятное. Может произойти так, что все четыре молекулы снова случайно окажутся в половине А, т.е. «газ», вначале расширившись, самопроизвольно сожмется. Т.е. процесс расширения оказался обратимым. Это может произойти довольно скоро для 4-х молекул из-за их высоких скоростей и быстрой смены состояний. Однако, вероятность такого события Такова вероятность того, что газ самопроизвольно сожмется в одной половине сосуда. А вероятность того, что молекулы равномерно распределятся по объему, растет с N. Таким образом, отсюда следует важный вывод: предоставленная самой себе макросистема стремится перейти от менее вероятных состояний к более вероятным. Это является причиной необратимости т. процессов. Обратимый процесс, в принципе, возможен, но его вероятность ничтожно мала. Таким образом, 2-ой закон термодинамики. указывает на необратимость перехода работы (механической энергии) в тепло, поскольку обратный переход – теплоты в работу означает переход от более вероятного состояния к менее вероятному. Понятие необратимости процессов применимо только для макросистем, для небольшого числа частиц оно неприменимо. Четыре молекулы возможно соберутся в одной половине сосуда, т.е. «газ» самопроизвольно сожмется. При большом N в состоянии равновесия число молекул в обоих половинах сосуда можно считать одинаковым.
|





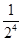 для 4х молекул и равна
для 4х молекул и равна 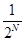 для N молекул, т.е. быстро уменьшается с ростом числа молекул. Если в сосуде N=100 молекул, то Р» 10-30.
для N молекул, т.е. быстро уменьшается с ростом числа молекул. Если в сосуде N=100 молекул, то Р» 10-30.


