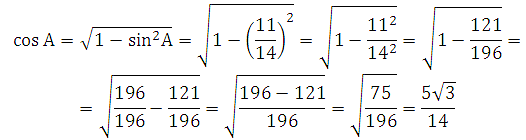Понятие синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике.
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла. Катеты — стороны, лежащие напротив острых углов.
Катет а, лежащий напротив угла альфа, называется противолежащим (по отношению к углу альфа). Другой катет b, который лежит на одной из сторон угла а, называется прилежащим. Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём. И наоборот: косинус одного острого угла в прямоугольном треугольнике равен синусу другого. Итого: основные соотношения для синуса, косинуса, тангенса и котангенса, которые пригодятся при решении задач:
Если в задаче на прямоугольный треугольник даны две стороны, сразу же находите третью, пригодится однозначно. Зная все три стороны, вы без труда найдёте значение любой тригонометрической функции (и любой угол).
В треугольнике ABC угол C равен 900,
Если в условии нет данных о сторонах и углах, а есть только тригонометрические функции, то пользуйтесь формулами:
Сразу видно, что можно использовать формулу:
Остаётся из основного тригонометрического тождества sin2A + cos2A = 1 найти cosA:
Таким образом:
Ответ: 0,25
В треугольнике ABC угол C равен 900,
Здесь необходимо найти тангенс другого острого угла. Как быть? Воспользуемся формулой тангенса:
Мы знаем, что в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла, и наоборот, то есть:
Найдём sin B. Из основного тригонометрического тождества sin2A + cos2A = 1 найдём cos A:
Значит
Таким образом:
Ответ: 0,25
В треугольнике ABC угол C равен 900, tg A = 7/24. Найдите sin A.
Используем формулу:
Из неё мы без труда найдём cos2A, а далее используя формулу основного тригонометрического тождества sin2A + cos2A = 1, сможем определить синус:
Вычислим sin A:
Ответ: 0,28 *Обратите внимание, что мы вычислили не косинус, а квадрат косинуса, так как далее для вычислений нам нужен именно квадрат.
В треугольнике ABC угол C равен 900, АВ = 8, sin A = 0,5. Найдите BC.
Здесь нам дана сторона (гипотенуза) и синус угла. Задача в одно действие, используется определение синуса:
Ответ: 4
В треугольнике ABC угол C равен 900, АВ = 7, tg =
В данной задаче через функцию тангенса мы можем выразить только катеты, но они нам неизвестны. Поэтому выразим её через функцию косинуса. Далее по определению косинуса, мы сможем найти АС, а затем по теореме Пифагора найдём ВС. Итак:
Следовательно:
По определению косинуса cos A = AC/АВ, значит можем найти АС:
Далее по теореме Пифагора вычислим ВС:
Таким образом, ВС = 4. Ответ: 4
В треугольнике ABC угол C равен 900, АС = 24, ВС = 7. Найдите sin A.
Если в задаче известны две стороны, то лучше сразу найти третью сторону по теореме Пифагора. Зная все три стороны в прямоугольном треугольнике, мы всегда без труда найдём значение любой тригонометрической функции любого угла. По теореме Пифагора:
По определению синуса:
Ответ: 0,28
В треугольнике ABC угол C равен 900,
По определению косинуса cos A = АС/АВ, значит:
Сторона АС нам известна, найдём cos A. Из основного тригонометрического тождества:
Таким образом:
Ответ: 28 Способов решения каждой подобной задачи не менее трёх.
Решите самостоятельно:
|


 Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе: Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: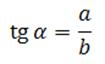 Другое (равносильное) определение – тангенсом острого угла называется отношение синуса угла к его косинусу:
Другое (равносильное) определение – тангенсом острого угла называется отношение синуса угла к его косинусу:

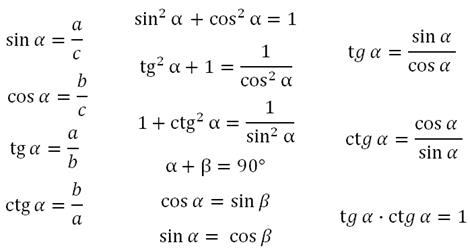

 Вывод: зная любые две стороны, мы можем найти третью сторону треугольника.
Вывод: зная любые две стороны, мы можем найти третью сторону треугольника.
 . Найдите tg A.
. Найдите tg A.
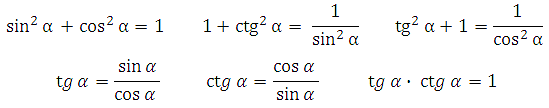
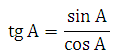
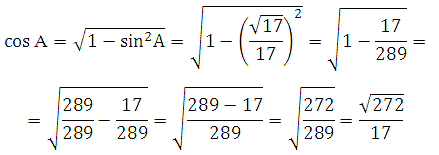
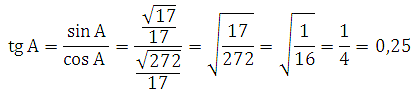
 . Найдите tg В.
. Найдите tg В.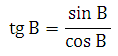

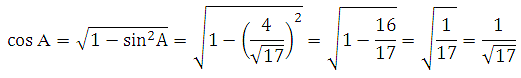
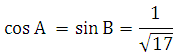


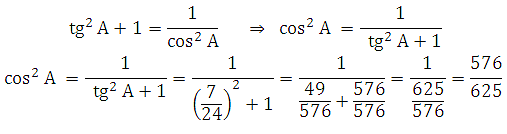


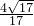 . Найдите ВC.
. Найдите ВC.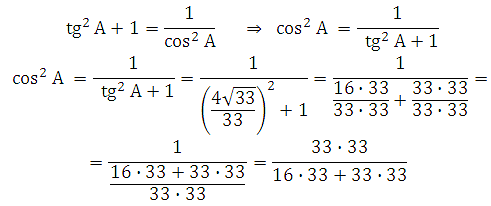
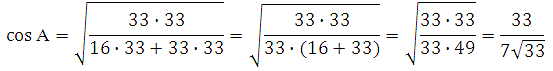
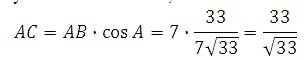
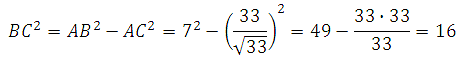
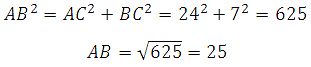

 , sin A = 11/14. Найдите AB.
, sin A = 11/14. Найдите AB.