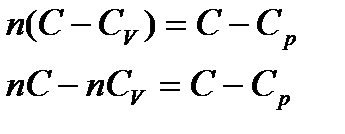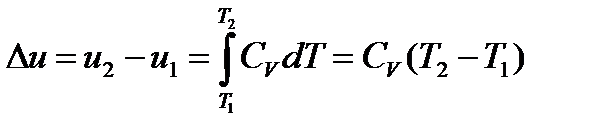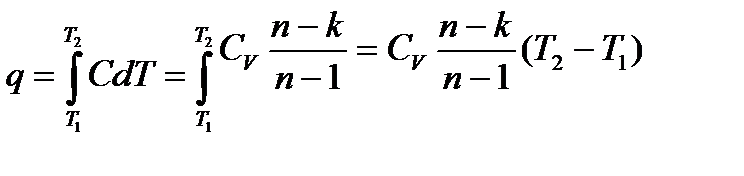Политропный процесс
Политропный процесс – это любой произвольный процесс, протекающий при постоянной теплоемкости, т.е.
Тогда, уравнение 1-го закона термодинамики примет вид
Таким образом, если C=const и CV=const,то количественное распределение теплоты между внутренней энергией и работой в политропном процессе остается постоянным (например 1:2). Доля теплоты, расходуемой на изменение внутренней энергии рабочего тела
Доля теплоты, расходуемая на внешнюю работу,
Получим уравнение политропного процесса. Для этого воспользуемся уравнением 1-го закона термодинамики (*)
или
Отсюда, из (*) и (**)
Разделив второе уравнение (4) на первое (3)
или
Введем величину
Интегрируя это выражение, получим
Это уравнение является уравнением политропы в pV− диаграмме. Показатель потлитропы n является постоянным для конкретного процесса, и может изменяться от -∞ до +∞. Пользуясь уравнением состояния, можем получить уравнение политропы в VT и pT – диаграммах. Из Из
Политропный процесс является обобщающим, а основные процессы (изохорный, изотермический, адиабатный) – частные случаи политропного процесса, каждому из которых соответствует свое значение n. Так, для каждого изохорного процесса n=±∞, изобарного n=0, изотермического n=1, адиабатного n=k. Поскольку уравнение политропы и адиабаты одинаковы по форме и отличаются только величиной n (показатель политропы вместо k−;показателя адиабаты), то можем записать − работа политропного процесса
− располагаемая работа политропного процесса
Теплоемкость газа из
Причем, в зависимости от n теплоемкость процесса может быть положительной, отрицательной, равной нулю и изменяется от -∞ до +∞. В процессах C<0 всегда l>q т.е. на выполнение работы расширения, кроме подведенной теплоты расходуется часть внутренней энергии газа. Изменение внутренней энергии политропного процесса
Теплота, сообщаемая газу в политропном процессе
Изменение энтальпии рабочего тела
|

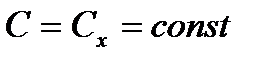
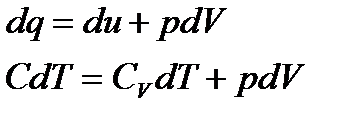 (*) (1)
(*) (1)
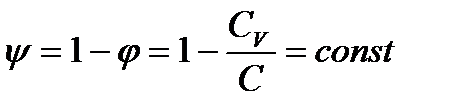

 (**) (2)
(**) (2) (3)
(3) (4)
(4)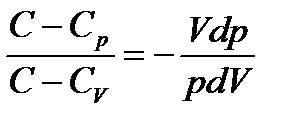

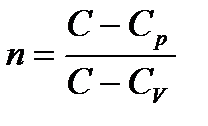 , называемою показателем политропы. Тогда,
, называемою показателем политропы. Тогда,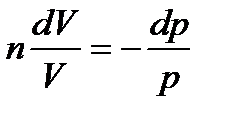
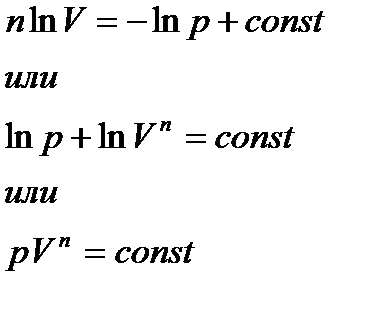
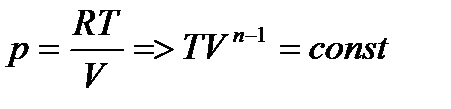 - уравнение политропы в VT- диаграмме.
- уравнение политропы в VT- диаграмме.

 − уравнение политропы в pT- диаграмме.
− уравнение политропы в pT- диаграмме.
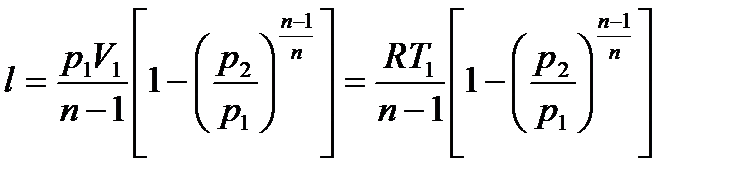
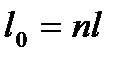
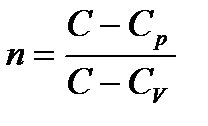 , откуда
, откуда