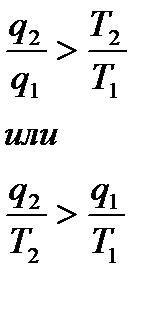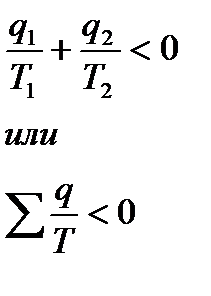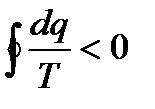Математическое выражение второго закона термодинамики.
Для получения математического выражения второго закона термодинамики вспомним термический к.п.д. цикла Карно. Для обратимого цикла Карно имеем термический к.п.д.
Отсюда,
− теплота взята по абсолютному значению. В последнем выражении теплота (q1 – это теплота) подводимая к рабочему телу, а q2 – теплота, отводимая от рабочего тела. Учитывая тогда что теплота q2 – отрицательна, запишем
или
Отношение Последнее равенство справедливо не только для цикла Карно, но и для любого обратимого цикла. Чтобы это показать рассмотрим в pV − диаграмме произвольный цикл.
Проведем большое количество близко расположенных адиабат, которые разобьют произвольный цикл на бесконечно большое кол-во элементарных циклов abcd, befc и т.д. Каждый такой цикл состоит из двух адиабат ad и bc; bc и ef и т.д. и двух элементарных отрезков контура цикла ab и cd; bc и fc и т.д. Поскольку эти отрезки бесконечно малы, то изменение температуры в них будет бесконечно малым, а следовательно приближенно можно считать эти отрезки изотермами, а образованные элементарные циклы – циклами Карно. Работа расширения по адиабате bc цикла abcd равна работе сжатия адиабаты c вцикле befc. Таким образом, адиабатные процессы не влияют на величину работы произвольного процесса. Теплота в этих адиабатных процессах не подводится и не отводится. То есть суммарное действие этих циклов одинаково с действием цикла 1-2-3-4. Для каждого цикла Карно справедливо соотношение (*). Суммируя эти соотношения для всех элементарных циклов
Переходя к пределу
Если интеграл по замкнутому контуру равен нулю, то подынтегральное выражение представляет собой полный дифференциал некоторой функции состояния. В термодинамике принято считать отношение
или
Для произвольной массы
Единицы измерения удельной энтропии (отнесенной к 1кг) Выражение (**) представляет собой математическое выражение второго закона термодинамики для обратимого цикла и называется первым интегралом Клаузиуса (получено им в 1834г.). Для необратимого цикла термический к.п.д. меньше чем к.п.д. цикла Карно, т.е.
и
Отсюда,
Учитывая, что теплота q2 – величина отрицательная, можем записать
Таким образом, алгебраическая сумма приведенных теплот для необратимого цикла Карно меньше нуля. Для произвольного необратимого цикла, состоявшего из бесконечно большого количества необратимых элементарных циклов (аналогично как мы делали с обратимым циклом), получим
Последнее неравенство представляет собой математическое выражение второго закона термодинамики для произвольно необратимого цикла и называется вторым интегралом Клаизиуса.
|

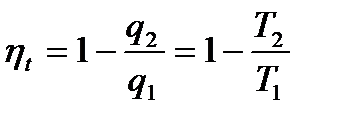 .
.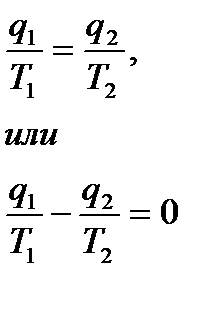
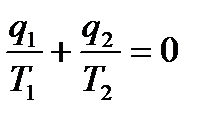
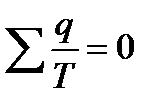 (*)
(*)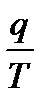 называется приведенной теплотой. Таким образом, в обратимом цикле Карно алгебраическая сумма приведённых теплот равна нулю.
называется приведенной теплотой. Таким образом, в обратимом цикле Карно алгебраическая сумма приведённых теплот равна нулю.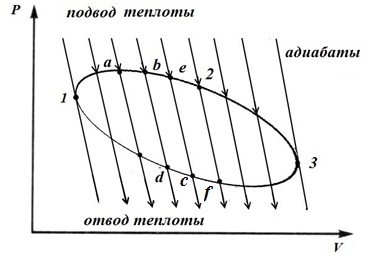
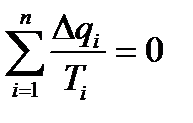
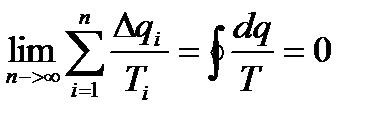 (**)
(**)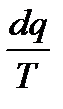 полным дифференциалом функции состояния S так называемой энтропией, т.е.
полным дифференциалом функции состояния S так называемой энтропией, т.е.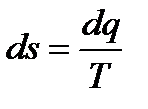
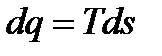 (s маленькое, удельная энтропия)
(s маленькое, удельная энтропия)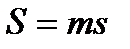
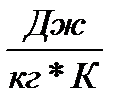 , для произвольной массы
, для произвольной массы 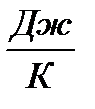 .
.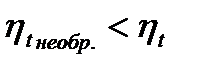

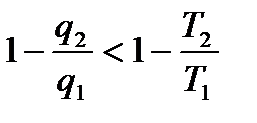 .
.