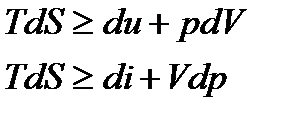Изменение энтропии в обратимых и необратимых процессах.
Рассмотрим вначале изменение энтропии в обратимых термодинамических процессах. Изменение энтропии в таких процессах
Температура всегда является положительной величиной. Поэтому при подводе теплоты, когда dq>0, то и dS>0, следовательно энтропия будет возрастать. Если теплота отводится от системы, то dq<0, dS<0 и энтропия убывает. Если проинтегрировать это уравнение, от начального состояния 1 до конечного 2, то изменение энтропии
Изменение энтропии будет равно нулю в процессах: − В обратимом адиабатном процессе dq=0,поэтому − В обратимых процессах в изолированной системе Для обратимых процессов имеем
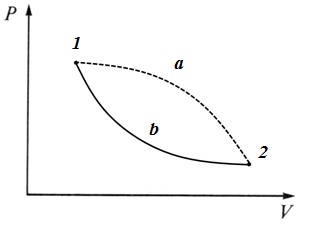
В изолированной системе изменение внутренней энергии du=0 и работа такой системы dl=0, а поскольку T>0,то dS=0 или S=const. Рассмотрим теперь изменение энтропии в необратимых процессах. Пусть некоторый произвольный цикл состоит из двух процессов: необратимого 1 a 2 и обратимого 2 b 1. Такой цикл будет необратимым.
Для такого цикла, согласно второму интегралу Клаузиуса, имеем
Для обратимого процесса 2- b -1имеем
Тогда, подставляя (**) в (*),
То есть в необратимом процессе значение интеграла Переходя, к дифференциальной форме записи
или
− в общем случае. Также как и интегралы Клаузиуса последнее неравенство представляет собой уравнение второго закона термодинамики, в котором знак равенства относится к обратимым процессам, а знак неравенства – к необратимым процессам. Дальше воспользуемся первым законом термодинамики
С учетом того, что
получим
Последние два уравнения содержат только термические параметры, функции состояния и их дифференциалы. Они объединяют первых и второй законы термодинамики и называются термодинамическим тождеством или объединенными уравнениями термодинамики.
|

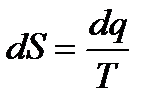 .
.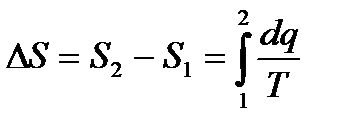
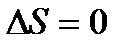 , т.е.
, т.е.  .
.
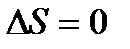
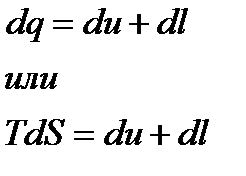
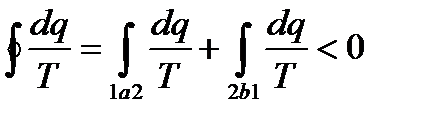 (*)
(*)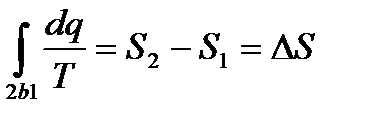 (**)
(**)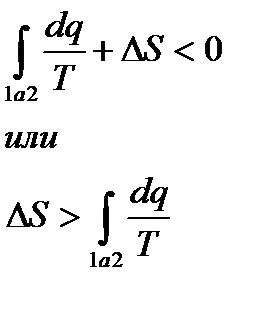
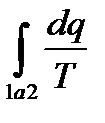 меньше, чем изменение энтропии в конечном и начальном состояниях.
меньше, чем изменение энтропии в конечном и начальном состояниях.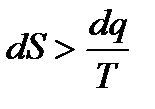
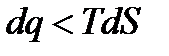
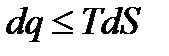
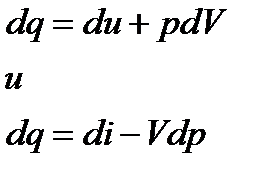
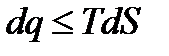 ,
,