Закон возрастания энтропии. Физический смысл энтропии.
Рассмотрим не обратимый процесс адиабатного расширения идеального газа в вакууме, температура газа при этом не изменяется T=const (закон Джоуля), поскольку внутренняя энергия не измена. Энтропия газа в начальном состоянии 1
Энтропия газа в объеме V2 после расширения
Изменения энтропии системы
Поскольку V2>V1, то ∆S>0 и S2>S1,т.е. энтропия системы возрастает, причем ∆q=0, поэтому увеличение энтропии происходит, только за счет уменьшения плотности газа (увеличение удельного объема). Вообще, все самопроизвольные процессы сопровождаются возрастанием энтропии.
То есть в этих процессах система переходит в состояние с большей энтропией. Последнее неравенство называется законом возрастания энтропии. Энтропия системы возрастает до тех пор, пока система не придет в состояние устойчивого равновесия (рассмотрим позже). При равновесии энтропия имеет максимально значение и постоянна. То есть, энтропия является критерием направления термодинамических процессов протекающих в изолированной системе, а ее приращение – мерой необратимости процесса. Таким образом, второй закон термодинамики для необратимых процессов указывает направление естественных процессов: естественные процессы протекают в направлении возрастания энтропии. Рассмотрим теперь необратимый круговой процесс и покажем, что возрастание энтропии приводит к уменьшению работоспособности системы, т.е. к деградации энергии. Допустим, что в изолированной системе совершается цикл Карно в интервале температур от T1 до T2. Работа цикла
q1− подведенная теплота. Предположим, что одновременно совершается необратимый цикл Карно, причем необратимость вызвана тем, что тоже количество теплоты q1 передается рабочему телу при температуре T1'<T1 (T1 – температура нагревателя). То есть нужно более высокая температура для передачи того же кол-ва теплоты, а часть теплоты теряется.
Поскольку T1'<T1, то ηt '< ηt и поэтому l'<l, т.е. в результате перехода теплоты на более низкий температурный уровень получается потеря работы (деградация энергии). Эта потеря равна
Энтропия системы в результате перехода теплоты q1 от нагревателя с температурой T1 к рабочему телу с температурой T1’ изменится на
Поскольку T1>T1’, то ∆S>0, т.е. энтропия возрастает. Из последних двух выражений
То есть потеря работы равна произведению абсолютной низшей температуры T2 на увеличение энтропии. Связь между возрастанием энтропии и уменьшением работы системы является общей для всех необходимых процессов. Для выяснения физического смысла энтропии приведем некоторые примеры. Сравним выражение для различных видов энергии. Кинетическая энергия определяется уравнением Каждое из этих уравнений содержит два множителя. Один характеризует качество или напряженность энергии (ω2 − квадрат скорости, H – высота подъема груза, T – температура, p −давление), а второй – выражает количество или ёмкость тела по отношению к данной энергии (m– масса тела, V−;удельный объем, S– энтропия). Первый множитель является интенсивным фактором, а второй – экстенсивным. То есть энтропия представляет собой емкость термодинамической системы по отношению к тепловой напряженности Клаузиус дал формулировки первого и второго законов термодинамики. 1. Энергия Вселенной постоянна. 2. Энтропия Вселенной стремится к максимуму. Таким образом, это должно привести к тепловой смерти Вселенной, когда температура выровняется. Но это противоречит, тому, что закон возрастания энтропии получен для изолированной системы.
|

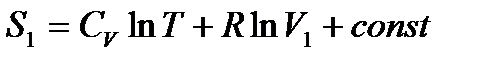
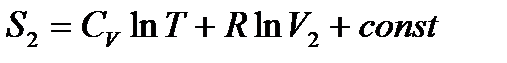
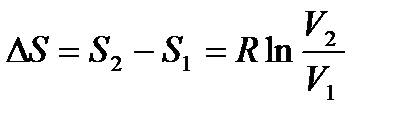
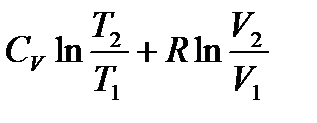
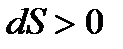
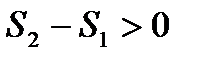
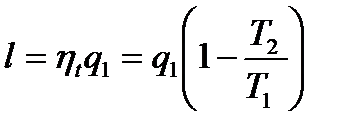
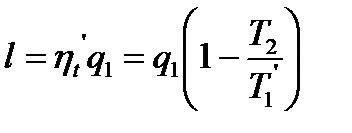
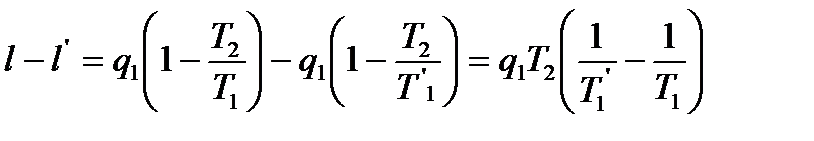

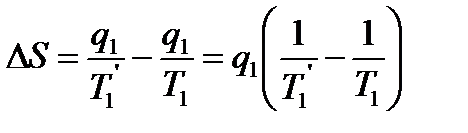
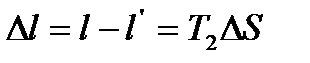 ,
,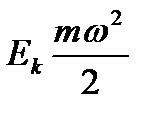 , потенциальная
, потенциальная 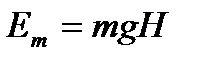 , работа по изменению объема тела dl=pdV, тепловая энергия dq=TdS.
, работа по изменению объема тела dl=pdV, тепловая энергия dq=TdS. .
.


