по нисходящему ряду можно воспользоваться про-
ведением вспомогательной линии длиной 10 см за
пределами поля эскиза (рис. 14). На основании
наблюдений, зарисовок, этюдов у автора возник
замысел: показать на картине опушку леса. Вни-
мание зрителя в первую очередь привлекает ель.
Все остальные деревья дополняют пейзаж и обра-
зуют стройное гармоническое целое, легко воспри-
нимаемое глазом. Такое гармоническое целое
создается благодаря расположению ели на линии
золотого сечения, а остальных деревьев или групп
деревьев — в должном порядке. Подсказывают этот
порядок (ритм) отрезки нисходящего ряда золо-
того сечения для данной картины, найденные при
помощи вспомогательной линии и отложенные на
пропорциональной линейке (для ширины и высо-
ты). Дальнейшая работа над пейзажем пойдет «на
глаз», по чувству. Пусть художественный вкус
автора, опыт и талант поведут его к успешному
завершению картины, к наилучшему выражению
замысла. Как в архитектуре, так и в живописи
геометрию привлекают для нужд пропорциониро-
вания, для создания предварительной схемы, ком-
позиционного каркаса, но не более.
Таблица 1. величины нисходящего ряда золотой пропорции
Ряд
| 1-й
| 2-й
| 3-й
| 4-й
|
|
|
|
|
|
|
|
| 61,8
| 61,803
|
|
|
| 38,2
| 38,196
|
|
|
| 23,6
| 23,606
|
| |
| 14,5
| 14,589
|
| |
| 9,0
| 9,017
|
| | | 5,5
| 5,572
|
| | | 3,5
| 3,444
|
| | | 2,0
| 2,128
|
| | | 1.5
| 1,315 0,813 0,502 0,311 и т. д.
|
Для нахождения отрезков золотой пропорции
восходящего и нисходящего рядов можно пользо-
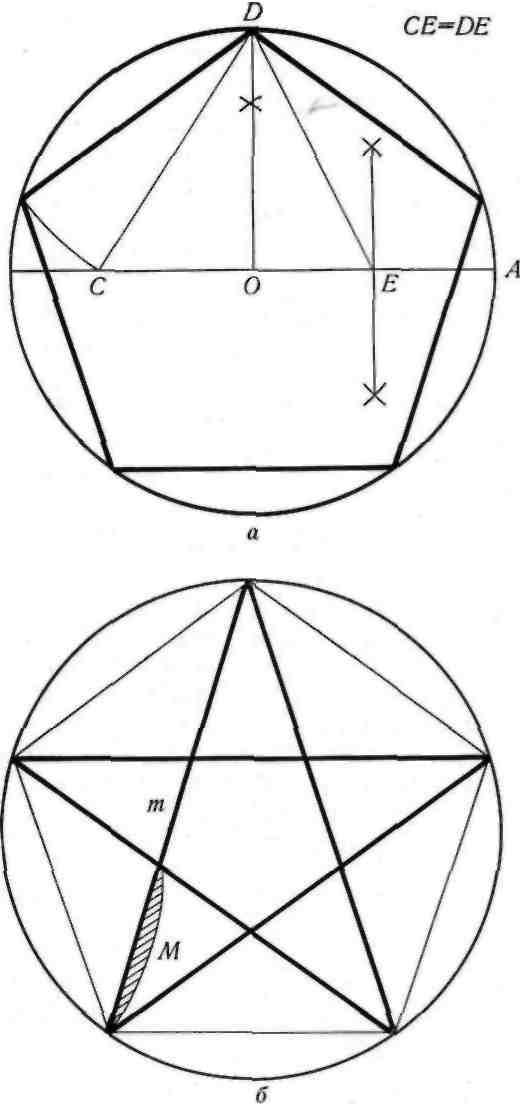
ваться пентаграммой (рис. 15). Для построения
пентаграммы необходимо построить правильный
пятиугольник. Способ его построения разработал
немецкий живописец и график Альбрехт Дюрер
(1471 — 1528) (рис. 15, а). Пусть О — центр окруж-
ности, А — точка на окружности и Е — середина
отрезка ОА. Перпендикуляр к радиусу ОА, вос-
ставленный в точке О, пересекается с окружностью
в точке D. Пользуясь циркулем, отложим на диа-
метре отрезок CE = ED. Длина стороны вписанного
в окружность правильного пятиугольника рав-
на DC. Откладываем на окружности отрезки DC
и получаем пять точек для начертания правильного
пятиугольника. Соединяем углы пятиугольника
через один диагоналями и получаем пентаграмму
(рис. 15, б). Все диагонали пятиугольника делят
друг друга на отрезки, связанные между собой
золотой пропорцией. Проводим прямую произволь-
ной длины, откладываем на ней отрезок m, ниже
откладываем отрезок М. На основании этих двух
отрезков выстраиваем шкалу отрезков золотой
пропорции восходящего и нисходящего рядов
(рис. 15, в).
Если размер эскиза не задан, берут любые два
значения шкалы как ширину или высоту эскиза
и находят все остальные величины, как было пока-
зано ранее.
Из всего сказанного вытекает, что художник,
желающий осуществить гармонический пропорцио-
| Рис. 16.
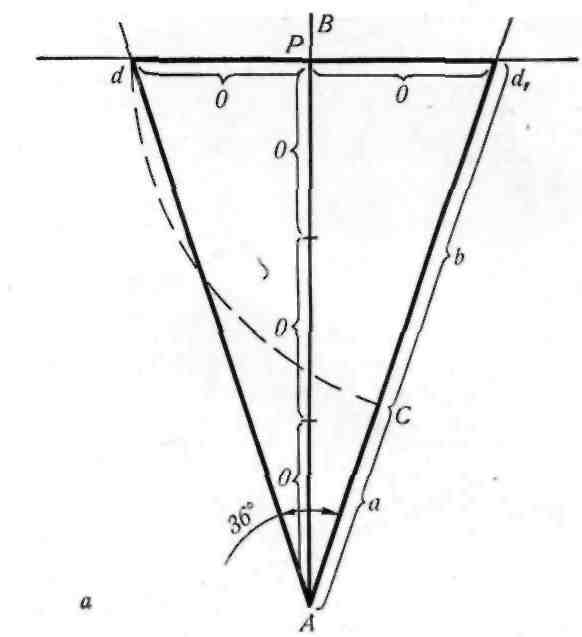
Построение: а —золотого треугольника: а:в =Ф, в=dd1 ; б — золотого прямоугольника: а: в = Ф
|
Рис. 15.
Построение правильного пятиугольника (а), пентаграммы (б)
и шкалы отрезков (в) золотой пропорции
нальный строй своей картины на основании золо-
того сечения, обязательно находит первые два
отрезка золотой пропорции. Решению этой задачи
способствует и золотой треугольник. Каждый конец
пятиугольной звезды представляет собой золотой
треугольник. Его стороны образуют угол 36° при
вершине, а основание, отложенное на боковую сто-
рону, делит ее в пропорции золотого сечения. Для
построения золотого треугольника' не требуется
даже транспортир (рис. 16, а). Проводим пря-
мую АВ. От точки А откладываем на ней три раза
отрезок О произвольной величины, через получен-
ную точку Р проводим перпендикуляр к линии АВ,
на перпендикуляре вправо И влево От точки Р
откладываем отрезки О. Полученные точки d и d\
соединяем прямыми с точкой А. Отрезок dd\ откла-
дываем на линию Ad\, получая точку С. Она раз-
делила линию Ad1 в пропорции золотого сечения.
Линиями Ad\ и dd\ пользуются для построения золо-
того прямоугольника (рис. 16, б).