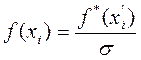Лабораторная работа № 1. Было произведено 844 измерения значения силы тока на выходе одного из нормирующих преобразователей
Было произведено 844 измерения значения силы тока на выходе одного из нормирующих преобразователей. Результаты были разбиты на 18 интервалов шириной ∆ = 0,003 мА и приведены в таблице №1. Там же указаны число измерений ni в каждом интервале и границы интервалов в миллиамперах. Таблица №1
Постройте гистограмму приведенного статистического ряда и произведите его выравнивание нормальным законом распределения
Задача выравнивания заключается в том, чтобы подобрать теоретическую кривую распределения, наилучшим образом описывающую экспериментальное статистическое распределение. Например, метод моментов заключается в подборе нескольких важнейших числовых характеристик (моментов) теоретического распределения, равных соответствующих моментам экспериментального распределения. Если для выравнивания используется нормальный закон, то такими числовыми характеристиками являются математическое ожидание x0 и дисперсия D, которые должны быть равны соответствующим статистическим характеристикам
где k – число разрядов (в нашем случае k = 18); pi - частота i-го разряда, представляющая отношение числа измерений ni в данном интеграле к общему числу измерений n (в нашем случае n = 844); xi – представитель i – го разряда (обычно принимается значение, соответствующее середине интервала). Для нашего случая получаем
Статистическую дисперсию
После вычисления получаем Таким образом, параметры нормального закона будут
а уравнение нормального закона примет вид
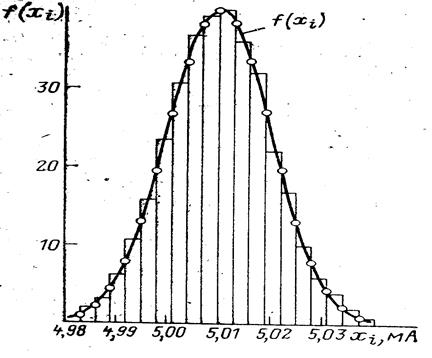
Рис.1
Гистограмма и выравнивающая её кривая распределения представлены на рис.1. При построении гистограммы следует иметь в виду, что составляющие её прямоугольники имеют основанием интервала ∆i, а площадь их равна частоте разряда pi, т.е. высота i – го прямоугольника li = pi/∆i. Теоретическую кривую распределения удобно строить путем вычисления значений на границах интервалов. Определяются значения аргумента x i, для границ интервалов
По таблицам определяются значения функции для соответствующих значений
после чего определяются значения плотности распределения x i на границах интервалов
Из рис.1 видно, что теоретическая кривая распределения сохраняет в основном особенности статистического распределения. Количественная оценка соответствия теоретического распределения к экспериментальному производится с помощью специальных критериев согласия.
|

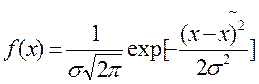
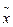 и
и 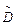 . При большом числе измерений среднее значение можно вычислить по приближенной формуле:
. При большом числе измерений среднее значение можно вычислить по приближенной формуле: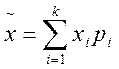 ,
,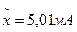 .
.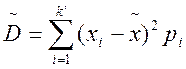 .
.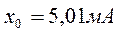 и
и 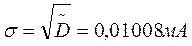 ,
,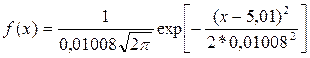 .
. 
 .
.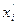
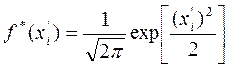 ,
,