Лабораторная работа № 3
ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ПРИ ПРЯМЫХ ИЗМЕРЕНИЯХ. Методика обработки результатов прямых измерений. Последовательность вычислений при обработке результатов прямых измерений. Предположим, что некоторая неизменная величина измеряется с помощью ряда отдельных наблюдений, выполняемых с одинаковой тщательностью и в одинаковых условиях (такой ряд называется равноточным). В итоге получено n результатов, несколько отличающихся друг от друга числовыми значениями: x1, x2, x3,…, xn. Поскольку проводится измерение определенного параметра конкретного объекта, то существует некоторое истинное значение этого параметра, которое невозможно определить из-за погрешностей отдельных наблюдений. Аналогичная совокупность значений xi может быть получена в результате измерения одного и того же параметра некоторого множества объектов, которые по идее должны быть абсолютно одинаковы, но в виду погрешностей, как изготовления, так и измерения, отличающихся друг от друга. Такой ряд называется стохастическим; его отличие от предыдущего состоит в том, что истинного значения измеряемого параметра не существует, так как оно является математической абстракцией, а каждый объект имеет свое значение этого параметра. Статистическая обработка выборок выполняется в такой последовательности: ü исключить (или уменьшить) систематические составляющие погрешности из результатов наблюдений; ü проверить соответствие экспериментального закона распределения теоретическому, нормальному (аналитическим или графическим способом). В случае, если можно предполагать, что данная выборка является частью генеральной совокупности, распределенному закону, обработка продолжается; ü вычислить наиболее вероятное значение x искомой величины; ü вычислить среднеквадратичное отклонение s результата наблюдения; ü при подозрении анормальности некоторого результата наблюдения xk, заметно отличающихся от остальных в выборке, вычислить показатель анормальности Vk для этого результата и сопоставить его с табличной величиной β для данного объема выборки. Если подозрения подтвердятся, этот результат наблюдения xk должен быть из выборки исключен, значения ü вычислить коэффициент вариации υ; для данной выборки; ü вычислить среднеквадратичное отклонение результата измерения ü вычислить доверительные границы ε; случайной составляющей погрешности результата измерения; ü вычислить доверительные границы θ не исключенных остатков систематической составляющей погрешности результата измерения; ü вычислить доверительные границы общей погрешности результата измерения (с учетом случайной и систематической составляющих); ü записать результат прямого измерения. Если одновременно обрабатываются две совокупности результатов многократных измерений однородных физических величин и эти результаты предполагается сравнивать между собой, необходимо установить, настолько статистически достоверны различия между этими выборками. Аналитический способ проверки соответствия опытного распределения нормальному. Поскольку рассмотренная статистическая обработка результатов наблюдений основана на использовании нормального закона распределения случайных величин, необходимо прежде всего убедиться, не противоречит ли распределение этих результатов в данной выборке нормальному закону. (Это должно быть сделано до начала статистической обработки, - непосредственно после исключения систематической погрешностей). При сравнительно небольшом числе наблюдений такую проверку можно выполнить аналитическим способом – с помощью «критерия W» (по СТ СЭВ 1190-78). Расчет с помощью «критерия W» выполняется для выборок объемом от 3 до 50 результатов наблюдений. При этом необходимо, прежде всего, упорядочить выборку, расположив все наблюдения xi в неубывающем порядке (в виде вариационного ряда): x1 £ x2 £ … £ xn. Исходные данные следует записать в расчетную таблицу (Табл. 3). Таблица № 3
В нижней половине третьей графы таблицы снизу вверх записываются значения j от 1 до l, причем l=n/2, если n четное, и l=(n-1)/2 при нечетном n. Из приложения 8 при соответствующих n и l следует найти значения коэффициента an-l+1 для j от 1 до l и записать их снизу вверх в графе 4, а затем подсчитать разности xn-j+1-xj, которые должны быть внесены в графу 5. Результаты построчного перемножения содержимого граф 4 и 5 записываются в графе 6 таблицы. Вычисляются характеристики
и Отсюда критерий
Задавшись определенным уровнем значимости α, отображающим наибольшую вероятность ошибочности гипотезы о принадлежности данной выборки к нормальной генеральной совокупности, по таблице в приложении 8 находим значение W*. При W>W* можно предполагать, что гипотеза справедлива, и опытное распределение не противоречит нормальному закону. При W<W* опытное распределение не соответствует нормальному закону. При вычислении значения φ2 на микро ЭВМ вычитание двух близких чисел
С целью снижения операционных ошибок целесообразно для вычисления φ2 пользоваться соотношением
Здесь c – произвольное целое число, не превышающее наименьшего значения ∆xi, но возможно более близкое к нему. Графоаналитический способ проверки соответствия опытного распределения нормальному предполагает использование вероятностной сетки, на которой по определенным правилам строится график эмпирического распределения (для анализируемой выборки). По конфигурации этого графика можно судить о том, соответствует ли опытное распределение нормальному закону (ГОСТ 11.008-75). Существует несколько вариантов такого построения. Наиболее удобный из них – с простыми вычислениями и прямолинейным графиком для нормального закона распределения. Данный вариант может применяться в выборках с числом наблюдений от 3 до 40. Как и предыдущем случае, выборку следует упорядочить и записать в табл. 5. Если какое – либо значения результатов наблюдений в таком вариационном ряду повторяются несколько раз, в таблицу они записываются только по одному разу, но указывается количество этих одинаковых значений (частота nj данной варианты xj упорядоченной выборки); для неповторяющихся значений xj частота nj=1. В следующей графе записываются нарастающим итогом так называемые «накопленные частоты» Nj (сумма значений nj от начала до данной xi включительно; для последней υ - й строки Nυ=n), после чего вычисляются значения интеграла Лапласа
Зная Ф(yj), по таблицам можно найти соответствующие значения yj. Для этого может быть использована таблица (прил. 2) однако удобнее воспользоваться специальной «обратной» таблицей (прил. 10). Для каждой пары значений xj и yj следует отметить точку в прямоугольной координатной системе с равномерной шкалой (xj – по оси абсцисс, yj – по ординат); соединив точки получим график функции yj=φ(xj). Если этот график приблизительно прямолинеен, то данная выборка не противоречит нормальному закону распределения. Если же графике криволинеен, выборка не соответствует нормальному закону. По форме кривой можно приближенно судить о характере закона распределения рис. 3: правосторонняя асимметрия означает, что у кривой деформирована, вытянута правая ветвь; при левосторонней асимметрии – растянута левая ветвь).
Вычисление наиболее вероятного значения результата измерения. Наиболее вероятным значением искомого результата является среднее арифметическое выборки:
Вычисление среднеквадратичного отклонения (СКО) результата наблюдения. Выборочное СКО результат наблюдений вычисляется обычно по формуле Бесселя. Эта формула не очень удобна для машинных вычислений, однако несложными алгебраическими преобразованиями её можно привести к более приемлемому для расчетов на микроЭВМ виду:
или (с целью снижения операционных погрешностей)
где ui=xi-c. Сопоставление соотношений (1) и (2) позволяет еще более упростить расчеты, воспользовавшись вычисленным ранее значением φ2:
Вычисленное СКО результата наблюдения можно вычислить по формуле Петерса. При этом, поскольку формула Бесселя справедлива для любого закона распределения погрешностей, а формула Петерса – только для нормального закона, сравнение величин, вычисленных по этим формулам (sБ и sП соответственно), можно использовать для приближенной оценки соответствия опытного распределения – теоретическому нормальному: если SБ и SП совпадают, выборка не противоречит нормальному распределению. Коэффициент вариации представляет собой относительную величину выборочного СКО результата наблюдения, %: υ=100 Оценка анормальности отдельных результатов наблюдений. Если рассматриваемая выборка в целом принадлежит к нормальному распределению, но возникают подозрения в анормальности некоторого отдельного наблюдения xk, результат которого заметно отличается от остальных, следует воспользоваться критерием анормальности результатов наблюдений (ГОСТ 11.002 – 73).Вычисляется показатель анормальности
Затем задавшись вероятностью γ, для данного объема выборки n из прил.11 находят параметр β (βn=2,7). Если результат xk принадлежит к данной нормальной совокупности, то с вероятностью γ можно утверждать, что абсолютное значение показателя анормальности Vk не превысит β. Следовательно, критерием анормальности является условие Vk ≥ β. Если это условие соблюдается, вероятность данного результата наблюдения xk меньше 1-γ;. Следовательно, он анормален и должен быть исключен из данной выборки (после чего значения Вычисление среднеквадратичного отклонения результат измерения. В формуле
величина Определение доверительной границы случайной составляющей погрешности результата измерения. Доверительный интервал случайной составляющей измерения обычно расположен симметрично относительно
Коэффициент доверия tγ в общем случае зависит от объема выборки n и принятой вероятности γ; значения его вычисленные на основании распределения Стьюдента, даны в прил. 6 (здесь число степеней свободы k=n-1). При n≥30 значение коэффициента доверия уже мало зависит от объема выборки; для вероятности γ=0,95 можно в соответствии с распределением Гаусса полагать, что tγ≈2. Определение доверительной границы не исключенных остатков систематической составляющей погрешности результата измерения. При тщательной попытки исключить систематическую составляющую погрешности какая – то часть её все равно останется не исключенной. Доверительную границу θ; этих остатков можно вычислить в результате анализа условий проведения эксперимента (например, не исключенная погрешность метода измерения, пределы допускаемой погрешности и пределы дополнительных погрешностей для средства измерения и т.д.) Таких не исключенных остатков может быть несколько (θi их доверительные границы). Если значения θi существенно отличаются друг от друга (например, на два порядка или больше), то меньшие из них следует отбросить, а оставшиеся просуммировать:
где θi – граница i – й не исключительной систематической погрешности; m – число этих составляющих; K – коэффициент, зависящий от принятой доверительной вероятности, числа составляющих и соотношения между ними. Для доверительной вероятности γ=0,95 при m£4 принимают коэффициент К=1,1. Определение доверительной границы общей погрешности результата измерения. Доверительная граница ∆А общей погрешности результата измерения А при наличии совокупности как не исключенной систематической, так и случайной составляющих погрешностей, в соответствии с ГОСТ 8.207 – 76 производится в зависимости от отношения величин θ; и при величиной θ; пренебрегают и читают, что ∆А = ε;; при ∆А = 0; при
Из формулы (*) можно вычислить максимальное число наблюдений, которые целесообразно провести в данных условиях (при СКО результатов наблюдений, в равном s, и наличии не исключенных остатков систематической составляющей с границей θ;) на основании следующих рассуждений: при увеличении n значение
Запись результата прямого измерения. Результат прямого измерения записывается согласно ГОСТ 8.011 – 62 в виде
|

 и s вычислены заново (для этой же выборки, но без xk);
и s вычислены заново (для этой же выборки, но без xk);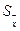 ;
;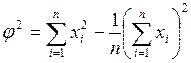
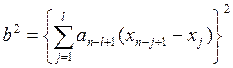 .
. .
. и
и  приводит к появлению большой операционной ошибки. Так, для массива, состоящего из n величин xi, не значительно отличающихся друг от друга (можно представить их как
приводит к появлению большой операционной ошибки. Так, для массива, состоящего из n величин xi, не значительно отличающихся друг от друга (можно представить их как 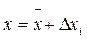 ), значение φ2 должно определяться только совокупностью ∆xi, но не зависеть от абсолютного значения
), значение φ2 должно определяться только совокупностью ∆xi, но не зависеть от абсолютного значения  .
. .
.
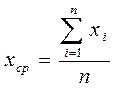 .
.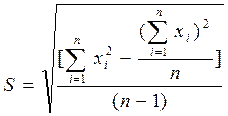 (1)
(1) , (2)
, (2)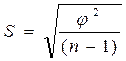 . (3)
. (3) .
.
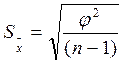
 характеризует точность
характеризует точность 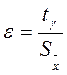

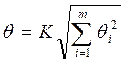 ,
,
 (*) пренебрегают величиной ε, и
(*) пренебрегают величиной ε, и доверительная граница ∆А вычисляется по формуле:
доверительная граница ∆А вычисляется по формуле: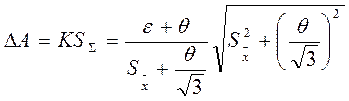 .
.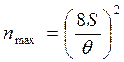 .
.



