Лабораторная работа № 2. С целью исследования закона распределения ошибки измерения концентрации кислорода газоанализатором было выполнено 315 измерений
С целью исследования закона распределения ошибки измерения концентрации кислорода газоанализатором было выполнено 315 измерений. Совокупность погрешностей представлена в виде статистического ряда (табл.№2).
Таблица №2
| ∆С,%
| 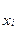
| ni
| pi
| ∆С,%
| 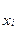
| ni
| pi
| | -0,50 ÷ -0,45
| -0,475
|
| 0,0381
| 0 – 0,05
| 0,025
|
| 0,05714
| | -0,45 ÷ -0,40
| -0,425
|
| 0,06032
| 0,05 – 0,10
| 0,75
|
| 0,06032
| | -0,40 ÷ -0,35
| -0,375
|
| 0,05397
| 0,10 – 0,15
| 0,125
|
| 0,04762
| | -0,35 ÷ -0,30
| -0,325
|
| 0,04762
| 0,15 – 0,20
| 0,175
|
| 0,05079
| | -0,30 ÷ -0,25
| -0,275
|
| 0,05079
| 0,20 – 0,25
| 0,225
|
| 0,04127
| | -0,25 ÷ -0,20
| -0,225
|
| 0,04444
| 0,25 – 0,30
| 0,275
|
| 0,05397
| | -0,20 ÷ -0,15
| -0,175
|
| 0,05714
| 0,30 – 0,35
| 0,325
|
| 0,05079
| | -0,15 ÷ -0,10
| -0,125
|
| 0,0381
| 0,35 – 0,40
| 0,375
|
| 0,05079
| | -0,10 ÷ -0,05
| -0,075
|
| 0,05079
| 0,40 – 0,45
| 0,425
|
| 0,04444
| | -0,05 ÷ -0
| 0,025
|
| 0,04127
| 0,45 – 0,50
| 0,475
|
| 0,06032
|
Производите выравнивание с помощью закона равномерной плотности и проверьте согласованность теоретического и статистического распределений с помощью критерия χ2. Доверительную вероятность того, что значения χ2, полученное по опытным данным, будет меньше соответствующего значения (χ*)2 теоретического распределения, принять равной p=0,05. Для этой вероятности при k=17
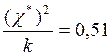 , ,
при k=18
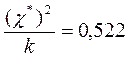 , ,
при k=19
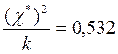 , ,
где k-число степеней свободы.
Закон равномерной плотности определяются выражением
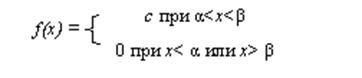
где 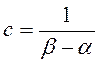 . .
Математическое ожидание и дисперсия подсчитываются по формулам
 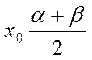 ; ; 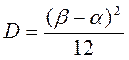 . .
При выравнивании следует выбрать α и β таким образом, чтобы х0 и D были равны статистическому среднему 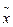 и статистической дисперсии и статистической дисперсии 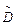 . В нашем случае . В нашем случае
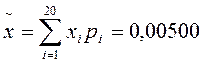 ; ;
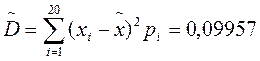 . .
Следовательно, 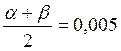 ; ; 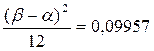 , откуда , откуда
α = - 0,5415 и β=0,05515.
Таким образом, 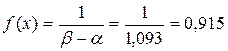 . .
На рис.№2 представлена гистограмма и выравнивающий её закон равномерной поверхности f(x).
Для поверки соответствия опытного распределения теоретическому используем критерий χ2.
Для этого вычисляем значение критерия χ2. По формуле
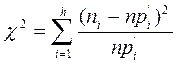 , ,
где h - число интервалов; ni – число наблюдений в i -ом интервале; n – общее число наблюдений; 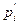 - теоретическая (т.е. в соответствии с выбранным теоретическим законом распределения) вероятность попадания в i -ый интервал. - теоретическая (т.е. в соответствии с выбранным теоретическим законом распределения) вероятность попадания в i -ый интервал.
Рис. 2

Для закона равномерной плотности при одинаковой плотности при одинаковых интервалах вероятность попадания 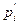 будет одинакова для всех интервалов: будет одинакова для всех интервалов:
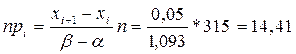
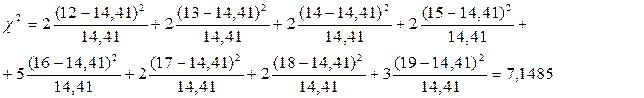
Определим число степеней свободы s. Оно определяется как число интервалов минус число наложенных связей. В нашем случае число наложенных связей равно трем.
Первая – сумма частот равна единице:
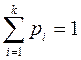 , ,
вторая – теоретическое и статистическое (экспериментальное) среднее значения должны быть равны:
 ; ;
третья – теоретическая и статистическая дисперсия должны быть равны:
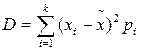 . .
Следовательно, в нашем случае число степеней свободы s = 20 – 3 = 17.
Вычисляем 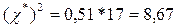 . Так как . Так как 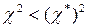 , то гипотеза о согласовании теоретического и экспериментального распределений считается правдоподобной. , то гипотеза о согласовании теоретического и экспериментального распределений считается правдоподобной.

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|

Логические цифровые микросхемы Более сложные элементы цифровой схемотехники (триггеры, мультиплексоры, декодеры и т.д.) не имеют...
|
Приложение Г: Особенности заполнение справки формы ву-45
После выполнения полного опробования тормозов, а так же после сокращенного, если предварительно на станции было произведено полное опробование тормозов состава от стационарной установки с автоматической регистрацией параметров или без...
Измерение следующих дефектов: ползун, выщербина, неравномерный прокат, равномерный прокат, кольцевая выработка, откол обода колеса, тонкий гребень, протёртость средней части оси
Величину проката определяют с помощью вертикального движка 2 сухаря 3 шаблона 1 по кругу катания...
Неисправности автосцепки, с которыми запрещается постановка вагонов в поезд. Причины саморасцепов ЗАПРЕЩАЕТСЯ: постановка в поезда и следование в них вагонов, у которых автосцепное устройство имеет хотя бы одну из следующих неисправностей:
- трещину в корпусе автосцепки, излом деталей механизма...
|
Устройство рабочих органов мясорубки Независимо от марки мясорубки и её технических характеристик, все они имеют принципиально одинаковые устройства...
Ведение учета результатов боевой подготовки в роте и во взводе Содержание журнала учета боевой подготовки во взводе. Учет результатов боевой подготовки - есть отражение количественных и качественных показателей выполнения планов подготовки соединений...
Сравнительно-исторический метод в языкознании сравнительно-исторический метод в языкознании является одним из основных и представляет собой совокупность приёмов...
|
|

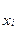
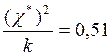 ,
,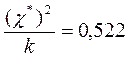 ,
,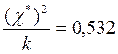 ,
,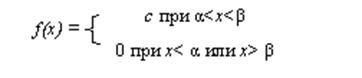
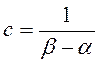 .
.
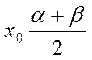 ;
; 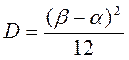 .
.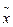 и статистической дисперсии
и статистической дисперсии 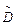 . В нашем случае
. В нашем случае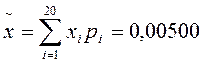 ;
;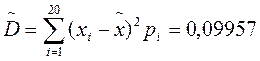 .
.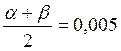 ;
; 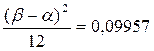 , откуда
, откуда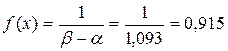 .
.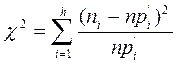 ,
,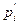 - теоретическая (т.е. в соответствии с выбранным теоретическим законом распределения) вероятность попадания в i -ый интервал.
- теоретическая (т.е. в соответствии с выбранным теоретическим законом распределения) вероятность попадания в i -ый интервал.
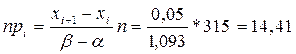
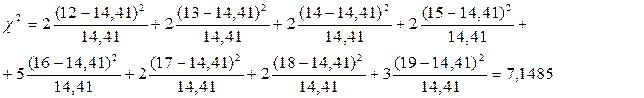
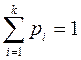 ,
, ;
;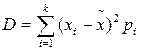 .
.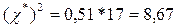 . Так как
. Так как 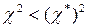 , то гипотеза о согласовании теоретического и экспериментального распределений считается правдоподобной.
, то гипотеза о согласовании теоретического и экспериментального распределений считается правдоподобной.


