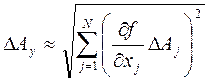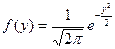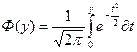Лабораторная работа № 4. Методика обработки результатов косвенных измерений.
ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ПРИ КОСВЕННЫХ ИЗМЕРЕНИЯХ.
Методика обработки результатов косвенных измерений.
Последовательность вычислений при обработке косвенных измерений. Исходными данными при косвенных измерениях являются ряды результатов наблюдений аргументов Xj, предварительно по методике, рассмотренной в лабораторной работе № 3 (проверка нормальности распределения, оценка анормальности).
Методика обработки результатов косвенных измерений может использоваться только при условии постоянства аргументов и отсутствия взаимной связи между ними. Поэтому перед началом вычислений надо, проанализировав попарно все результаты наблюдений аргументов, убедиться в отсутствии корреляции между ними. Если корреляционная связь не обнаружена, производится дальнейшая обработка: определяется результат косвенного измерения и оценивается погрешность.
В особо ответственных случаях вычисление погрешности результата производиться следующим образом:
ü определяется оценка случайной составляющей погрешности результата (на основании случайных составляющих погрешностей аргументов);
ü определяется оценка исключительных остатков систематической составляющей погрешности результата;
ü определяются доверительные границы общей погрешности результата косвенного измерения (по композиции законов распределения случайной и не исключенной систематической составляющих погрешности).
Такой расчет весьма сложен; однако в большинстве технических измерений вполне удовлетворительные результаты могут быть получены более простыми способами.
Проверка отсутствия корреляции между результатами наблюдений каждой пары аргументов. Коэффициент корреляции R между аргументами Xh и Xl вычисляется по формуле:
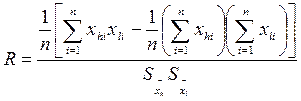 , (1) , (1)
где n – число наблюдений; xhi и xli – результаты i – го наблюдения соответственно h – го и l – го аргументов; 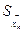 и и 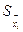 - оценки среднеквадратичного отклонения результатов измерения этих аргументов. - оценки среднеквадратичного отклонения результатов измерения этих аргументов.
Для уменьшения операционных погрешностей при вычислениях на микроЭВМ следует вместо xi использовать величины ui= xi - c. Тогда подставив в формулу (1) значения 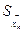 и и 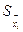 , получим , получим
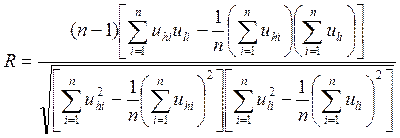 . (2) . (2)
Здесь uhi = xhi – ch; uli = xli – cl.
Затем вычисляется показатель корреляции
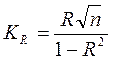 (3) (3)
Критерием отсутствия корреляции является неравенство:
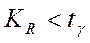 , (4) , (4)
где tγ – коэффициент доверия (прил. 7) при доверительной вероятности γ и числе степеней свободы k = n – 1.
Если неравенство (4), то это означает, что корреляционная связь между данной парой аргументов Xh и Xl отсутствует. При наличии корреляционной зависимости между аргументами обработки экспериментальных данных при косвенных измерениях производится более сложной методике (см. специальную литературу).
Определение результата косвенного измерения. При отсутствии корреляционной связи между результатами наблюдений аргументов среднее значение результата косвенного измерения можно найти, подставляя в уравнение связи средние значения результатов прямых измерений этих аргументов:
 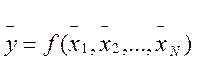 (5) (5)
Зависимость погрешности результата косвенного измерения от погрешностей аргументов. Погрешность результата косвенного измерения в общем случае определяется соотношением:
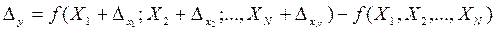 , (6) , (6)
где Xj – истинные значения аргументов; ∆xj – погрешности измерения этих аргументов.
Однако полученное выражение неудобно для практического использования. Разложив в ряд Тейлора, получим приблизительную формулу:
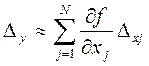 , (7) , (7)
где ∂f/∂xj – частная производная от y из уравнения связи по j – му измеряемому аргументу; ∆xyj – абсолютная погрешность прямого измерения j – го аргумента.
В реальных условиях при сложении погрешностей возможна их частичная взаимная компенсация, поэтому формула (7) дает несколько завышенные результаты; вероятность наихудшего сочетания погрешностей, при котором все они арифметически складываются, с ростом N стремится к нулю. Поэтому лучшие результаты получаются среднеквадратичным суммированием погрешностей:
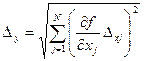 . (8) . (8)
Величину Еj=(∂f/∂xj)∆xj называется частной погрешностью результата косвенного измерения.
Определение погрешности результата косвенного измерения для наиболее распространенных уравнений связи. Из формулы (8) можно вывести значения погрешности результата косвенного измерения для некоторых часто встречающихся уравнений связи, например, для функции одной переменной, для суммы или произведения аргументов и т.п.
Для функции одной переменной
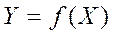 (9) (9)
абсолютная погрешность результата составляет
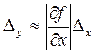 ; (10) ; (10)
в частном случае, если 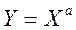 , то , то 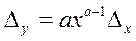 . .
Это выражение удобнее представить в виде относительной погрешности результата:
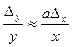 . (11) . (11)
Из формулы (11) следует, что возведение в степень значительно увеличивает погрешность результата, поэтому измерение величин, которые при дальнейших вычислениях возвышаются в степень, должно производиться с особой точностью.
Если 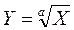 , то , то
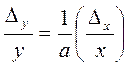 . (12) . (12)
Следовательно, величины, из которых при дальнейшей обработке извлекаются корни, могут измеряться с меньшей точностью, поскольку погрешность таких величин при обработке уменьшается.
Для алгебраической суммы
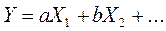 ; (13) ; (13)
абсолютная погрешность результата
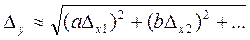 . (14) . (14)
Для произведения
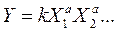 ; (15) ; (15)
погрешности результата
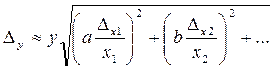 , (16) , (16)
В формулах (13)-(16) величины a и b, … - любые целые или дробные, положительные или отрицательные числа.
Определение доверительных границ погрешностей результата косвенного измерения. Если при проведении прямых измерений аргументов систематическая составляющая их погрешности была невелика (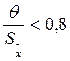 ), то её влиянием можно пренебречь. В этом случае следует вычислить среднеквадратичную погрешность ), то её влиянием можно пренебречь. В этом случае следует вычислить среднеквадратичную погрешность 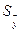 результата косвенного измерения: результата косвенного измерения:
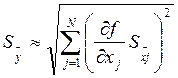 , (17) , (17)
где 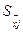 - среднеквадратичные погрешности результатов прямых измерений аргументов xj. - среднеквадратичные погрешности результатов прямых измерений аргументов xj.
Затем вычисляется так называемое «эффективное число степеней свободы» для данного косвенного измерения:
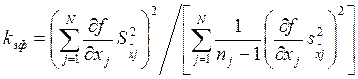 , (18) , (18)
где nj – число прямых измерений аргумента xj.
Если все nj одинаковы и равны n, то
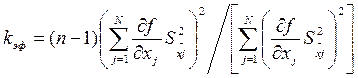 . (19) . (19)
В прил. 7, задавшись значениями γ, находим для k = kэф (если значения kэф получилось дробным, его следует округлить) величину tγ, после чего вычисляем доверительные границы случайной составляющей погрешности результата косвенного измерения:
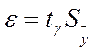 . (20) . (20)
В этом случае доверительная граница общей погрешности результата косвенного измерения
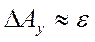 . (21) . (21)
Если при проведении прямых измерений аргументов из систематической составляющей погрешности пренебречь нельзя, то доверительную границу общей погрешности результата косвенного измерения можно приближенно определить подставляя в формулу (8) значения доверительных границ ∆Аj общих погрешностей результатов прямых измерений аргументов xj (все ∆Аj должны определяться при одинаковой доверительной вероятности γ):
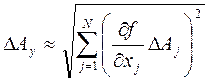
Приложения.
Приложение 1. Плотность стандартного нормального распределения
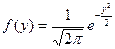
| y
| f(y)
| y
| f(y)
| y
| f(y)
| |
| 0,3989
| 1,4
| 0,1497
| 2,8
| 0,0079
| | 1,5
| 0,1295
| 2,9
| 0,006
| | 1,6
| 0,1109
|
|
| | 0,1
| 0,397
| 1,7
| 0,094
|
| 0,0044
| | 0,2
| 0,391
| 1,8
| 0,079
| | 0,3
| 0,3814
| 1,9
| 0,0656
| | 0,4
| 0,3683
|
| 0,054
| 3,1
| 0,0033
| | 0,5
| 0,3621
| 3,2
| 0,0024
| | 0,6
| 0,3332
| 3,3
| 0,0017
| | 0,7
| 0,3123
| 2,1
| 0,044
| 3,4
| 0,0012
| | 0,8
| 0,2897
| 2,2
| 0,0355
| 3,5
| 0,0009
| | 0,9
| 0,2661
| 2,3
| 0,0283
| 3,6
| 0,0006
| |
| 0,242
| 2,4
| 0,0224
| 3,7
| 0,0004
| | 2,5
| 0,0175
| 3,8
| 0,0003
| | 2,6
| 0,0136
| 3,9
| 0,0002
| | 1,1
| 0,2179
| 2,7
| 0,0104
|
| 0,0001
| | 1,2
| 0,1942
| | 1,3
| 0,1714
|
Приложение 2. Интеграл Лапласа 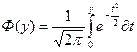
| y
| f(y)
| y
| f(y)
| y
| f(y)
| y
| f(y)
| y
| f(y)
| y
| f(y)
| | 0,00
|
| 0,4
| 0,1554
| 0,8
| 0,2881
| 1,2
| 0,3849
| 1,55
| 0,4394
| 1,9
| 0,4713
| | 0,01
| 0,004
| 0,41
| 0,1591
| 0,81
| 0,291
| 1,21
| 0,3869
| 1,56
| 0,4406
| 1,91
| 0,4719
| | 0,02
| 0,008
| 0,42
| 0,1628
| 0,82
| 0,2939
| 1,22
| 0,3888
| 1,57
| 0,4418
| 1,92
| 0,4726
| | 0,03
| 0,012
| 0,43
| 0,1664
| 0,83
| 0,2967
| 1,23
| 0,3907
| 1,58
| 0,443
| 1,93
| 0,4732
| | 0,04
| 0,016
| 0,44
| 0,17
| 0,84
| 0,2995
| 1,24
| 0,3925
| 1,59
| 0,4441
| 1,94
| 0,4738
| | 0,05
| 0,0199
| 0,45
| 0,1736
| 0,85
| 0,3023
| 1,25
| 0,3944
| 1,6
| 0,4452
| 1,95
| 0,4744
| | 0,06
| 0,0239
| 0,46
| 0,1772
| 0,86
| 0,3051
| 1,26
| 0,3962
| 1,61
| 0,4453
| 1,96
| 0,475
| | 0,07
| 0,0279
| 0,47
| 0,1808
| 0,87
| 0,3078
| 1,27
| 0,398
| 1,62
| 0,4474
| 1,97
| 0,4756
| | 0,08
| 0,0319
| 0,48
| 0,1844
| 0,88
| 0,3106
| 1,28
| 0,3997
| 1,63
| 0,4484
| 1,98
| 0,4762
| | 0,09
| 0,0359
| 0,49
| 0,1879
| 0,89
| 0,3133
| 1,29
| 0,4015
| 1,64
| 0,4495
| 1,99
| 0,4767
| | 0,10
| 0,0398
| 0,5
| 0,1915
| 0,9
| 0,3159
| 1,3
| 0,4032
| 1,65
| 0,4505
|
| 0,4772
| | 0,11
| 0,0438
| 0,51
| 0,195
| 0,91
| 0,3186
| 1,31
| 0,4049
| 1,66
| 0,4515
| 2,01
| 0,798
| | 0,12
| 0,0478
| 0,52
| 0,1985
| 0,92
| 0,3212
| 1,32
| 0,4066
| 1,67
| 0,4525
| 2,02
| 0,4821
| | 0,13
| 0,0517
| 0,53
| 0,2019
| 0,93
| 0,3238
| 1,33
| 0,4082
| 1,68
| 0,4535
| 2,03
| 0,4842
| | 0,14
| 0,0557
| 0,54
| 0,2054
| 0,94
| 0,3264
| 1,34
| 0,4099
| 1,69
| 0,4545
| 2,04
| 0,4861
| | 0,15
| 0,0596
| 0,55
| 0,2088
| 0,95
| 0,3289
| 1,35
| 0,4115
| 1,7
| 0,4554
| 2,25
| 0,4878
| | 0,16
| 0,0636
| 0,56
| 0,2123
| 0,96
| 0,3315
| 1,36
| 0,4131
| 1,71
| 0,4564
| 2,3
| 0,4893
| | 0,17
| 0,0675
| 0,57
| 0,2157
| 0,97
| 0,334
| 1,37
| 0,4147
| 1,72
| 0,4573
| 2,35
| 0,4906
| | 0,18
| 0,0714
| 0,58
| 0,219
| 0,98
| 0,3365
| 1,38
| 0,4162
| 1,73
| 0,4582
| 2,4
| 0,4918
| | 0,19
| 0,0753
| 0,59
| 0,2224
| 0,99
| 0,3389
| 1,39
| 0,4177
| 1,74
| 0,4591
| 2,45
| 0,4929
| | 0,20
| 0,0793
| 0,6
| 0,2257
|
| 0,3413
| 1,4
| 0,4192
| 1,75
| 0,4599
| 2,5
| 0,4938
| | 0,21
| 0,0832
| 0,61
| 0,2291
| 1,01
| 0,3438
| 1,41
| 0,4207
| 1,76
| 0,4699
| 2,55
| 0,4946
| | 0,22
| 0,0871
| 0,62
| 0,2324
| 1,02
| 0,3461
| 1,42
| 0,4222
| 1,77
| 0,4616
| 2,6
| 0,4953
| | 0,23
| 0,091
| 0,63
| 0,2357
| 1,03
| 0,3485
| 1,43
| 0,4236
| 1,78
| 0,4625
| 2,65
| 0,496
| | 0,24
| 0,0948
| 0,64
| 0,2389
| 1,04
| 0,3508
| 1,44
| 0,4235
| 1,79
| 0,4633
| 2,7
| 0,4965
| | 0,25
| 0,0987
| 0,65
| 0,2422
| 1,05
| 0,3531
| 1,45
| 0,4265
| 1,8
| 0,4641
| 2,75
| 0,497
| | 0,26
| 0,1026
| 0,66
| 0,2454
| 1,06
| 0,3554
| 1,46
| 0,4278
| 1,81
| 0,4648
| 2,8
| 0,4974
| | 0,27
| 0,1064
| 0,67
| 0,2486
| 1,07
| 0,3557
| 1,47
| 0,4292
| 1,82
| 0,4656
| 2,85
| 0,4978
| | 0,28
| 0,1103
| 0,68
| 0,2517
| 1,08
| 0,3599
| 1,48
| 0,4306
| 1,83
| 0,4664
| 2,9
| 0,4981
| | 0,29
| 0,1141
| 0,69
| 0,2549
| 1,09
| 0,3621
| 1,49
| 0,4319
| 1,84
| 0,4671
| 2,95
| 0,4984
| | 0,30
| 0,1179
| 0,7
| 0,258
| 1,1
| 0,3643
| 1,5
| 0,4332
| 1,85
| 0,4678
|
| 0,4986
| | 0,31
| 0,1217
| 0,71
| 0,2611
| 1,11
| 0,3665
| 1,51
| 0,4345
| 1,86
| 0,4686
| 3,1
| 0,499
| | 0,32
| 0,1255
| 0,72
| 0,2642
| 1,12
| 0,3686
| 1,52
| 0,4357
| 1,87
| 0,4693
| 3,2
| 0,4993
| | 0,33
| 0,1293
| 0,73
| 0,2673
| 1,13
| 0,3708
| 1,53
| 0,437
| 1,88
| 0,47
| 3,3
| 0,4995
| | 0,34
| 0,1331
| 0,74
| 0,2703
| 1,14
| 0,3729
| 1,54
| 0,4382
| 1,89
| 0,4706
| 3,4
| 0,4997
| | 0,35
| 0,1368
| 0,75
| 0,2734
| 1,15
| 0,3749
|
|
|
|
|
| 0,4999
| | 0,36
| 0,1406
| 0,76
| 0,2764
| 1,16
| 0,377
|
|
|
|
|
|
| | 0,37
| 0,1443
| 0,77
| 0,2794
| 1,17
| 0,379
|
|
|
|
|
|
| | 0,38
| 0,148
| 0,78
| 0,2823
| 1,18
| 0,381
|
|
|
|
|
|
| | 0,39
| 0,1517
| 0,79
| 0,2852
| 1,19
| 0,383
|
|
|
|
|
|
|
Приложение 3. Квантили нормального распределения (при μ = 0 и σ = 1)
| γ;
| γ,%
| хγ
| γ;
| γ,%
| хγ
| | 0,0013
| 0,13
| -3
| 0,6
|
| 0,2019
| | 0,0025
| 0,25
| -2,807
| 0,7
|
| 0,5244
| | 0,005
| 0,5
| -2,5758
| 0,8
|
| 0,8416
| | 0,01
|
| -2,3263
| 0,9
|
| 1,2816
| | 0,0228
| 2,28
| -2
| 0,95
|
| 1,6499
| | 0,025
| 2,5
| -1,956
| 0,975
| 97,5
| 1,956
| | 0,05
|
| -1,6449
| 0,9772
| 97,72
|
| | 0,1
|
| -1,2816
| 0,99
|
| 2,3263
| | 0,2
|
| -0,8416
| 0,995
| 99,5
| 2,5758
| | 0,3
|
| -0,5244
| 0,9975
| 99,75
| 2,807
| | 0,4
|
| -0,2019
| 0,9987
| 99,87
|
| | 0,5
|
|
|
|
|
| Приложение 4. Коэффициент Мk
| k
| Мk
| k
| Мk
| k
| Мk
| |
| 1,253
|
| 1,025
|
| 1,013
| |
| 1,128
|
| 1,023
|
| 1,013
| |
| 1,085
|
| 1,021
|
| 1,01
| |
| 1,064
|
| 1,019
|
| 1,008
| |
| 1,051
|
| 1,018
|
| 1,007
| |
| 1,042
|
| 1,017
|
| 1,006
| |
| 1,036
|
| 1,016
|
| 1,006
| |
| 1,032
|
| 1,015
|
| 1,005
| |
| 1,028
|
| 1,014
|
| 1,004
| Приложение 5. Коэффициент dn
| n
| dn
| n
| dn
| n
| dn
| n
| dn
| |
| 0,886
|
| 0,351
|
| 0,294
|
| 0,268
| |
| 0,591
|
| 0,337
|
| 0,288
|
| 0,222
| |
| 0,486
|
| 0,325
|
| 0,283
|
| 0,199
| |
| 0,43
|
| 0,315
|
| 0,279
|
| 0,182
| |
| 0,395
|
| 0,307
|
| 0,275
|
| 0,165
| |
| 0,37
|
| 0,3
|
| 0,271
|
| 0,154
| Приложение 6. Коэффициент am
| m
| am
| m
| am
| m
| am
| |
| 0,8862
|
| 0,4299
|
| 0,3512
| |
| 0,5908
|
| 0,3946
|
| 0,3367
| |
| 0,4857
|
| 0,3698
|
| 0,3249
|
Приложение 7. Коэффициент доверия tγ
| k
| При γ;
| k
| При γ;
| | 0,95
| 0,99
| 0,999
| 0,95
| 0,99
| 0,999
| |
| 12,706
| 63,657
| 636,619
|
| 2,093
| 2,861
| 3,883
| |
| 4,303
| 9,925
| 31,598
|
| 2,086
| 2,845
| 3,85
| |
| 3,182
| 5,841
| 12,941
|
| 2,08
| 2,831
| 3,819
| |
| 2,776
| 4,604
| 8,61
|
| 2,074
| 2,819
| 3,792
| |
| 2,571
| 4,032
| 6,859
|
| 2,069
| 2,807
| 3,797
| |
| 2,447
| 3,707
| 5,959
|
| 2,064
| 2,797
| 3,745
| |
| 2,365
| 3,499
| 5,405
|
| 2,06
| 2,787
| 3,725
| |
| 2,306
| 3,355
| 5,041
|
| 2,056
| 2,779
| 3,707
| |
| 2,262
| 3,25
| 4,781
|
| 2,052
| 2,793
| 3,674
| |
| 2,428
| 3,169
| 4,587
|
| 2,048
| 2,763
| 3,674
| |
| 2,201
| 3,106
| 4,437
|
| 2,045
| 2,756
| 3,659
| |
| 2,179
| 3,055
| 4,318
|
| 2,042
| 2,75
| 3,646
| |
| 2,16
| 3,012
| 4,221
|
| 2,021
| 2,704
| 3,551
| |
| 2,145
| 2,977
| 4,14
|
| 2,008
| 2,677
| 3,497
| |
| 2,131
| 2,947
| 4,073
|
|
| 2,66
| 3,46
| |
| 2,12
| 2,921
| 4,015
|
| 1,99
| 2,639
| 3,416
| |
| 2,11
| 2,898
| 3,965
|
| 1,984
| 2,626
| 3,391
| |
| 2,101
| 2,878
| 3,922
| ∞
| 1,96
| 2,576
| 3,291
|
Приложение 8. Коэффициенты an-j+1
| j
| n
| |
|
|
|
|
|
|
| |
| 0,7071
| 0,6872
| 0,6646
| 0,6631
| 0,6233
| 0,6052
| 0,5888
| |
| -
| 0,1677
| 0,2413
| 0,2806
| 0,3031
| 0,3164
| 0,3244
| |
| -
| -
| -
| 0,0875
| 0,1401
| 0,1743
| 0,1976
| |
| -
|
| -
| -
| -
| 0,0561
| 0,0947
| | j
| n
| |
|
|
|
|
|
|
| |
| 0,5739
| 0,5601
| 0,5475
| 0,5359
| 0,5251
| 0,515
| 0,5056
| |
| 0,3291
| 0,3315
| 0,3325
| 0,3325
| 0,3318
| 0,3306
| 0,329
| |
| 0,2141
| 0,226
| 0,2347
| 0,2412
| 0,246
| 0,2495
| 0,2521
| |
| 0,1224
| 0,1429
| 0,1586
| 0,1707
| 0,1802
| 0,1878
| 0,1939
| |
| 0,0393
| 0,0695
| 0,0922
| 0,1099
| 0,124
| 0,1353
| 0,1447
| |
| -
| -
| 0,0303
| 0,0539
| 0,0727
| 0,088
| 0,1005
| |
| -
| -
| -
| -
| 0,024
| 0,0433
| 0,0593
| |
| -
| -
| -
| -
| -
| -
| 0,0196
| | j
| n
| |
|
|
|
|
|
|
| |
| 0,4968
| 0,4886
| 0,4808
| 0,4734
| 0,4643
| 0,459
| 0,4542
| |
| 0,3273
| 0,3253
| 0,3232
| 0,3211
| 0,3185
| 0,3157
| 0,3126
| |
| 0,254
| 0,2553
| 0,2561
| 0,2565
| 0,2578
| 0,2571
| 0,2563
| |
| 0,1988
| 0,2027
| 0,2059
| 0,2085
| 0,2119
| 0,2131
| 0,2139
| |
| 0,1524
| 0,1587
| 0,1641
| 0,1686
| 0,1736
| 0,1764
| 0,1787
| |
| 0,1109
| 0,1197
| 0,1271
| 0,1334
| 0,1399
| 0,1443
| 0,148
| |
| 0,0725
| 0,0837
| 0,0932
| 0,1013
| 0,1092
| 0,115
| 0,1201
| |
| 0,0359
| 0,0496
| 0,0612
| 0,0711
| 0,0804
| 0,0878
| 0,0941
| |
| -
| 0,0163
| 0,0303
| 0,0422
| 0,053
| 0,0618
| 0,0696
| |
| -
| -
| -
| 0,014
| 0,0263
| 0,0368
| 0,0459
| |
| -
| -
| -
| -
| -
| 0,0122
| 0,0228
| | j
| n
| |
|
|
|
|
|
|
| |
| 0,4493
| 0,445
| 0,4407
| 0,4366
| 0,4328
| 0,4291
| 0,4254
| |
| 0,3098
| 0,3069
| 0,3043
| 0,3018
| 0,2992
| 0,2968
| 0,2944
| |
| 0,2554
| 0,2543
| 0,2533
| 0,2522
| 0,251
| 0,2499
| 0,2487
| |
| 0,2145
| 0,2148
| 0,2151
| 0,2152
| 0,2151
| 0,215
| 0,2148
| |
| 0,1807
| 0,1822
| 0,1836
| 0,1848
| 0,1857
| 0,1864
| 0,187
| |
| 0,512
| 0,1539
| 0,1563
| 0,1584
| 0,1601
| 0,1616
| 0,163
| |
| 0,1245
| 0,1283
| 0,1316
| 0,1346
| 0,1372
| 0,1395
| 0,1415
| |
| 0,0997
| 0,1046
| 0,1089
| 0,1128
| 0,1162
| 0,1192
| 0,1219
| |
| 0,0764
| 0,0823
| 0,0876
| 0,0923
| 0,0965
| 0,1002
| 0,1036
| |
| 0,0539
| 0,061
| 0,0672
| 0,0728
| 0,0778
| 0,0822
| 0,0852
| |
| 0,0321
| 0,0403
| 0,0476
| 0,054
| 0,0598
| 0,065
| 0,0697
| |
| 0,0107
| 0,02
| 0,0284
| 0,0358
| 0,0424
| 0,0483
| 0,0537
| |
| -
| -
| 0,0094
| 0,0178
| 0,0253
| 0,032
| 0,0381
| |
| -
| -
| -
| -
| 0,0084
| 0,0159
| 0,0227
| |
| -
| -
| -
| -
| -
| -
| 0,0076
| Примечание. Для 30<n<50 значения коэффициентов an-j+1 приведены в СТ СЭВ 1190-78.
Приложение 9. Значения W* (для α = 0,95)
| n
| W*
| n
| W*
| n
| W*
| |
| 0,737
|
| 0,859
|
| 0,908
| |
| 0,748
|
| 0,866
|
| 0,911
| |
| 0,762
|
| 0,874
|
| 0,914
| |
| 0,788
|
| 0,881
|
| 0,916
| |
| 0,803
|
| 0,887
|
| 0,918
| |
| 0,818
|
| 0,892
|
| 0,92
| |
| 0,829
|
| 0,897
|
| 0,923
| |
| 0,842
|
| 0,901
|
| 0,924
| |
| 0,85
|
| 0,905
|
| 0,926
| |
|
|
|
|
| 0,927
| Примечание. Для 30<n<50 значения параметра W* приведены в СТ СЭВ 1190-78.
Приложение 10. Зависимость y от интеграла Лапласа Ф(y)
| Ф(y)
| y
| Ф(y)
| y
| Ф(y)
| y
| Ф(y)
| y
| | 0,01
| 0,025
| 0,16
| 0,41
| 0,31
| 0,88
| 0,46
| 1,75
| | 0,02
| 0,05
| 0,17
| 0,44
| 0,32
| 0,92
| 0,465
| 1,81
| | 0,03
| 0,075
| 0,18
| 0,47
| 0,33
| 0,95
| 0,47
| 1,88
| | 0,04
| 0,1
| 0,19
| 0,5
| 0,34
| 0,99
| 0,475
| 1,96
| | 0,05
| 0,13
| 0,2
| 0,52
| 0,35
| 1,04
| 0,48
| 2,05
| | 0,06
| 0,15
| 0,21
| 0,55
| 0,36
| 1,08
| 0,485
| 2,17
| | 0,07
| 0,18
| 0,22
| 0,58
| 0,37
| 1,13
| 0,49
| 2,33
| | 0,08
| 0,2
| 0,23
| 0,61
| 0,38
| 1,18
| 0,492
| 2,41
| | 0,09
| 0,23
| 0,24
| 0,64
| 0,39
| 1,23
| 0,494
| 2,51
| | 0,1
| 0,25
| 0,25
| 0,67
| 0,4
| 1,28
| 0,495
| 2,58
| | 0,11
| 0,28
| 0,26
| 0,71
| 0,41
| 1,34
| 0,496
| 2,65
| | 0,12
| 0,31
| 0,27
| 0,74
| 0,42
| 1,41
| 0,497
| 2,75
| | 0,13
| 0,33
| 0,28
| 0,77
| 0,43
| 1,48
| 0,498
| 2,88
| | 0,14
| 0,36
| 0,29
| 0,81
| 0,44
| 1,55
| 0,499
| 3,1
| | 0,15
| 0,39
| 0,3
| 0,84
| 0,45
| 1,64
| 0,4999
|
| Приложение 11. Значения β; (для γ; = 0,95)
| n
| β;
| n
| β;
| n
| β;
| n
| β;
| n
| β;
| |
| 1,15
|
| 2,11
|
| 2,41
|
| 2,58
|
| 2,68
| |
| 1,46
|
| 2,18
|
| 2,44
|
| 2,59
|
| 2,69
| |
| 1,67
|
| 2,23
|
| 2,48
|
| 2,61
|
| 2,69
| |
| 1,82
|
| 2,29
|
| 2,5
|
| 2,63
|
| 2,7
| |
| 1,94
|
| 2,33
|
| 2,53
|
| 2,65
|
|
| |
| 2,03
|
| 2,37
|
| 2,56
|
| 2,66
|
|
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
Примеры задач для самостоятельного решения. 1.Спрос и предложение на обеды в студенческой столовой описываются уравнениями: QD = 2400 – 100P; QS = 1000 + 250P
1.Спрос и предложение на обеды в студенческой столовой описываются уравнениями: QD = 2400 – 100P; QS = 1000 + 250P...
Дизартрии у детей Выделение клинических форм дизартрии у детей является в большой степени условным, так как у них крайне редко бывают локальные поражения мозга, с которыми связаны четко определенные синдромы двигательных нарушений...
Педагогическая структура процесса социализации Характеризуя социализацию как педагогический процессе, следует рассмотреть ее основные компоненты: цель, содержание, средства, функции субъекта и объекта...
|
Машины и механизмы для нарезки овощей В зависимости от назначения овощерезательные машины подразделяются на две группы: машины для нарезки сырых и вареных овощей...
Классификация и основные элементы конструкций теплового оборудования Многообразие способов тепловой обработки продуктов предопределяет широкую номенклатуру тепловых аппаратов...
Именные части речи, их общие и отличительные признаки Именные части речи в русском языке — это имя существительное, имя прилагательное, имя числительное, местоимение...
|
|

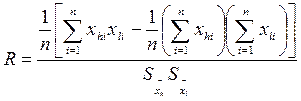 , (1)
, (1)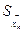 и
и 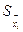 - оценки среднеквадратичного отклонения результатов измерения этих аргументов.
- оценки среднеквадратичного отклонения результатов измерения этих аргументов.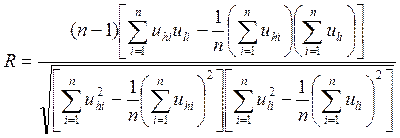 . (2)
. (2)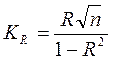 (3)
(3)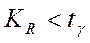 , (4)
, (4)
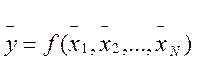 (5)
(5)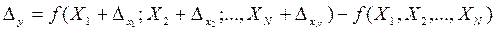 , (6)
, (6)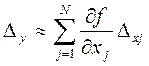 , (7)
, (7)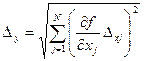 . (8)
. (8)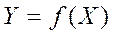 (9)
(9)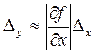 ; (10)
; (10)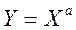 , то
, то 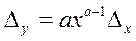 .
.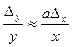 . (11)
. (11)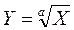 , то
, то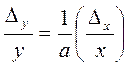 . (12)
. (12)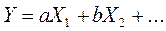 ; (13)
; (13)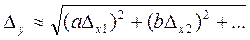 . (14)
. (14)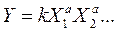 ; (15)
; (15)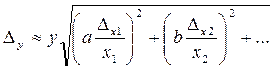 , (16)
, (16)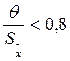 ), то её влиянием можно пренебречь. В этом случае следует вычислить среднеквадратичную погрешность
), то её влиянием можно пренебречь. В этом случае следует вычислить среднеквадратичную погрешность 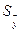 результата косвенного измерения:
результата косвенного измерения: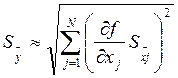 , (17)
, (17)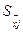 - среднеквадратичные погрешности результатов прямых измерений аргументов xj.
- среднеквадратичные погрешности результатов прямых измерений аргументов xj.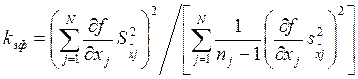 , (18)
, (18)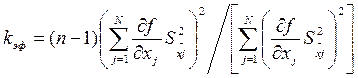 . (19)
. (19)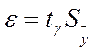 . (20)
. (20)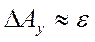 . (21)
. (21)