Понятие производной.Лекция 15. Производная.
Понятие производной.
Пусть функция Определение 15.1. Конечный предел отношения приращения Этот предел обозначается символом
Наряду с обозначением производной Конкретные значения производной при Формулу (15.1) можно записать в виде
J Пример 15.1.
|
определена в некоторой окрестности точки 
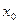. Дадим аргументу 
(положительное или отрицательное). Тогда функция 
. Рассмотрим отношение 
.
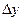функции 
называется производной функции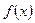 
в точке 
:
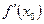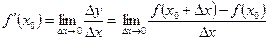. (15.1)
в произвольной точке x употребляются и другие обозначения: 
, 
, 
.
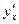обозначаются через 
, 
.
. (15.2)
. J
