♦ Теорема 15.1. Если функция  имеет производную в точке
имеет производную в точке 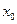 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Доказательство. Пусть существует производная в точке 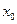 , то есть
, то есть
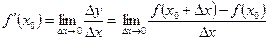 .
.
Тогда по замечанию 12.3 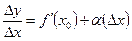 , где
, где 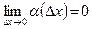 . Следовательно,
. Следовательно, 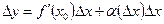 . Но тогда
. Но тогда
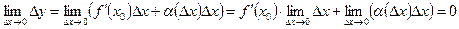 .
.
Это означает, что функция 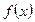 непрерывна в точке
непрерывна в точке 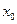 . ■
. ■
☼ Замечание 15.3. Обратное утверждение не всегда верно, то есть не всякая непрерывная в точке 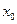 функция имеет производную в этой точке.☼
функция имеет производную в этой точке.☼
J Пример 15.2. Функция 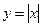 непрерывна в точке
непрерывна в точке 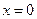 . Найдём
. Найдём
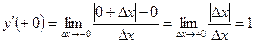 ,
,
 .
.
Таким образом, у функции 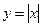 в точке
в точке 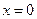 существуют односторонние производные, но они не равны и, следовательно, функция
существуют односторонние производные, но они не равны и, следовательно, функция 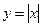 не имеет производной в точке
не имеет производной в точке 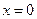 . J
. J
Если функция 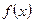 имеет производную в точке
имеет производную в точке 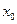 , то говорят, что
, то говорят, что 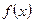 дифференцируема в этой точке.
дифференцируема в этой точке.

 имеет производную в точке
имеет производную в точке 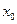 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.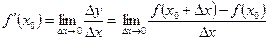 .
.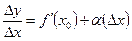 , где
, где 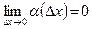 . Следовательно,
. Следовательно, 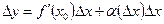 . Но тогда
. Но тогда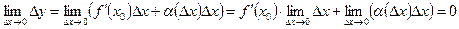 .
.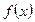 непрерывна в точке
непрерывна в точке 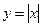 непрерывна в точке
непрерывна в точке 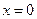 . Найдём
. Найдём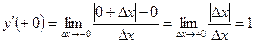 ,
, .
.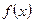 имеет производную в точке
имеет производную в точке 


