ЗАДАЧИ И УПРАЖНЕНИЯ
1. При игре в кости бросаются два игральных кубика и подсчитывается сумма выпавших очков. Найти вероятность событий: А - сумма равна 5; В - сумма равна 7. Ответ: Р(А) = 0,1111, Р(В) = 0,1667
2. Из имеющихся 15 телевизоров 10 готовы к продаже, а 5 требуют дополнительной регулировки. Найти вероятности событий: А - из случайно отобранных трёх телевизоров все хорошие, В - два хорошие и один нет, С - один хороший и два нет, D - хороших нет. Ответ: Р(А) = 0,2637, Р(В) = 0,4945, Р(С) = 0,2198, Р(D) = 0,022.
3. Из изготовленных N изделий M стандартные (M £ N). Найти вероятность того, что из n случайно отобранных изделий ровно m стандартные (m £ n). Ответ: Р(А) =
4. В студенческой группе из 30 студентов 20 успевают на хорошо и отлично, 5 - удовлетворительно и остальные плохо. Найти вероятность того, что из пяти случайно отобранных студентов: А - все успевают на хорошо и отлично; В - 3 хорошо и отлично, 1 удовлетворительно и 1 плохо; С - 3 удовлетворительно и 2 плохо. Ответ: Р(А) =0,1088, Р(В) = 0,2, Р(С) = 0,0007.
5. В книжной лотерее разыгрываются 30 билетов, из них 10 - выигрышные. Определить вероятность того, что из двух купленных билетов окажутся: А - оба выигрышные, В - один выигрышный, другой нет; С - оба проигрышные. Ответ: Р(А) = 0,1034, Р(В) = 0,4598, Р(С) = 0,4368.
6. Абонент забыл три цифры нужного ему телефонного номера и набирает их наудачу. Найти вероятность того, что номер будет набран правильно, если: А - абонент помнит, что все эти цифры различные, В - ничего не помнит об этих цифрах. Ответ: Р(А) = 0,0014, Р(В) = 0,001.
7. Две бригады получили 10 инструментов, из которых 2 новых и 8 старых. Найти вероятность того, при делении их случайным образом каждой бригаде достанется 1 новый и 4 старых. Ответ: Р(А) =0,5556. 8. В лотерее разыгрывается 30 билетов, из них 5 “счастливые”. Найти вероятность того, что из 4 купленных случайным образом билетов 2 будут счастливыми. Ответ: Р(А) = 0,1095.
9. В спортлото (5 из 36) надо отметить 5 чисел из 36. Найти вероятность того, что случайным образом удастся угадать: 0, 1, 2, 3, 4, 5 пять чисел из пять заранее выбранных (но не известных играющему) чисел. Ответ: Р(0) = 0,4507, Р(1) = 0,4173, Р(2) = 0,1192, Р(3) = 0,01233, Р(4) = 0,0004111, Р(5) = 0,000002653.
10. Рассматриваются всевозможные пятизначные числа. Найти вероятность того, что: А - случайно выбранное число записано различными цифрами; В - не содержит цифры 5. Ответ: Р(А) = 0,3024, Р(В) = 0,5832.
11. Студенческая группа состоит из 15 юношей и 4 девушек. По жребию (случайным образом) выбирают 4 дежурных. Найти вероятность того, что будут выбраны 2 девушки и 2 юноши. Ответ: Р(А) = 0,1625
12. В партии из 20 часов 3 дефектные. Найти вероятность того, что из 4 случайно купленных часов все хорошие. Ответ: Р(А) = 0,4912.
13. Имеются два цифровых замка. На первом размещено 6 дисков, на каждом из которых находится 5 символов; на втором - 5 дисков с 6 символами на каждом. Какой из них лучше? Ответ: Р(А) = 0,000064 < Р(В) = 0,000129 (первый лучше).
14. Буквы, составляющие слово РЕМОНТ выписаны каждая на отдельной карточке и тщательно перемешаны. Найти вероятность того, что: А - при последовательном отборе четырёх карточек сразу получится слово МОРЕ; В - из отобранных карточек можно составить это слово. Ответ: Р(А) = 0,002778, Р(В) = 0,06667.
15. На четырёх карточках выписаны две буквы М и две буквы А. Найти вероятность того, что при случайном отборе карточек сразу получится слово МАМА. Ответ: Р(А) =0,1667. 16. Буквы, составляющие слово ОДЕССА выписаны на отдельных карточках и тщательно перемешаны. Найти вероятность того, что при последовательном отборе трёх карточек появятся буквы составляющие слова: А - САД, В - АСС, С - ОСА; D - четырех карточек - слово СОДА. Ответ: Р(А) = 0,0167, Р(В) = 0,0167, Р(С) = 0,0167, Р(D) = 0,0056.
17. Решить предыдущую задачу считая, что по извлечённой карточке записывается буква, а сама карточка возвращается и все карточки снова тщательно перемешиваются. Ответ: Р(А) = 0,0093, Р(В) = 0,0185, Р(С) = 0,0093, Р(D) = 0,0015. 18. Сетка с прямоугольными ячейками сварена из прутков диаметром 1см, с горизонтальным шагом 10 и вертикальным - 15см. Найти вероятность того, что шарик радиуса 1см, брошенный не прицельно, перпендикулярно сетке, пройдёт через неё без столкновений. Ответ: Р(А) =0,56. 19. Перпендикулярно фарватеру установлен один ряд мин, расстояние между которыми равно 100 метров. Найти вероятность того, что: А - судно с наибольшей шириной 30м пройдёт линию заграждения без столкновения с миной; В - судно будет двигаться под углом 30о к фарватеру? Ответ: Р(А) = 0,7, Р(В) = 0,6564.
20. На отрезок АВ длины L брошена точка М так, что её любое положение на отрезке равновозможно. Найти вероятность того, что меньший из отрезков (АМ или МВ) имеет длину, большую чем L\3. Ответ: Р(А) = 0,3333.
21. Плоскость разделена параллельными прямыми на полосы шириной 10см каждая. На плоскость случайным образом брошен круг радиуса 2см. Найти вероятность того, что круг не пересечёт прямые. Ответ: Р(А) = 0,6.
22. На отрезок АВ длины L брошены точки М и N так, что любое их положение на этом отрезке равновозможно. Найти вероятность того, что длина отрезка MN меньше длины наименьшего из отрезков АМ или АN. Ответ: Р(А) = 0,5.
23. Задача о встрече. Два студента М и Д договорились встретиться в определённом месте между 18 и 19 часами. Если первым приходит М, то он ждёт не более 20 минут и затем уходит, если первой приходит Д, то ждёт не более 10 минут. Найти вероятность того, что встреча состоится, если каждый из них выбирает момент своего прихода наудачу. Ответ: Р(А) = 0,4306. 24. Пол выложен прямоугольными плитками размерами 15 на 20см. Найти вероятность того, что брошенная на пол случайным образом монета (круг радиуса 2см) не пересечёт границ одной плитки. Ответ: Р(А) = 0,5867.
Ответ: Р(А) = 0,6366, Р(В) = 0,4135.
26. Опыт заключается в случайном бросании точки на квадрат (достоверное событие W), а попадание точки в области А, В и С - есть события А, В и С. Указать (заштриховать соответствующую область) события:
27. На 30 километровом участке линии электропередачи после бури оказались повалены две опоры. Считая, что поваленной могла оказаться любая из опор, найти вероятность того, что между поваленными опорами будет не более двух километров, если опоры расставлены через каждые 100 метров. Ответ: Р(А) = 0,1318.
28. Первая задача шевалье д'Мере (решена Б.Паскалем). Найти вероятность выигрыша при игре в кости по следующим правилам: игрок выигрывает, если при бросании четырёх костей хотя бы на одной выпадет 6 очков, и проигрывает в противном случае. Ответ: Р(А) =0,5177 > 0,5.
29. Вторая задача шевалье д'Мере. Найти вероятность выигрыша при игре в кости по следующим правилам: игрок выигрывает, если при одновременном бросании двух костей 24 раза хотя бы один раз одновременно выпадут две шестёрки, и проигрывает в противном случае. Ответ: Р(А) = 0,491 < 0,5.
30. Сколько раз надо бросить две игральные кости, чтобы хотя бы один раз выпали одновременно две шестёрки с вероятностью не меньшей чем 0,5. Ответ: n ³ 25 (Р(А) = 0,5055 > 0,5). 31. Три стрелка делают по одному выстрелу в мишень. Вероятность попадания в цель у первого стрелка равна 0,9, у второго - 0,8 и у третьего - 0,6. Найти вероятность того, что в мишень попадут: три стрелка - событие А; два - В; один - С; ни один не попадёт Д; хотя бы один попадёт - Е. Ответ: Р(А) =0,432, Р(В) =0,444, Р(С) =0,116, Р(Д) =0,008, Р(Е) =0,992. 32. В группе N студентов. Найти вероятность того, что хотя бы у двух совпадают дни рождения. Проделать вычисления для N равного: А - 100, В - 60 и С - 30. Ответ: Р = 1 - 365 364... (365 - N +1) / 365. Р(А) =0,9999997, Р(В) =0,9941, Р(С) = 0,7063. 33. Для разрушения моста достаточно одного попадания из орудия. Найти вероятность разрушения моста, если из орудия можно сделать не более четырёх выстрелов, и вероятность попадания в цель при первом выстреле равна 0,3, при втором - 0,4, третьем - 0,5 и четвёртом - 0,7. Ответ: Р(А) =0,937. 34. Найти надёжность схем D и E, если надежность её элементов известна: Р(А) = 0,8, Р(В) =0,7 и Р(С) =0,4.
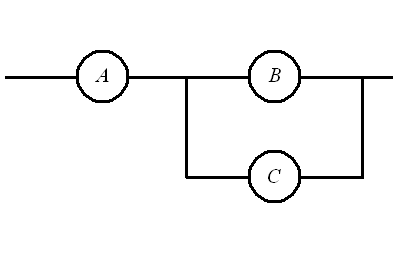
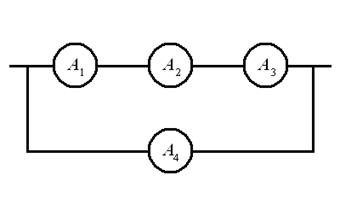
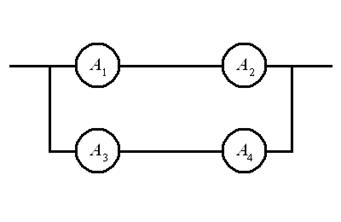
Ответ: Р(D) = 0,736, Р(Е) = 0,656. 35. Найти надёжность схем В, С, D и Е, если надёжность её элементов известна: Р(А1) =0,6, Р(А2) = 0,7, Р(А3) = 0,8 и Р(А4)= 0,9.
Ответ: Р(В) =0,5076, Р(С) =0,8624, Р(D) = 0,9336, Р(Е) =0,8376. 36. Из 30 вопросов, подготовленных к экзамену, студент успел выучить только 20. Найти вероятность того, что при случайном отборе трёх вопросов он получит: три хороших вопроса - событие А, два хороших и один плохой - В, один хороший и два плохих - С, все плохие - D. Ответ: Р(А) = 0,2808, Р(В) = 0,468, Р(С) = 0,2217, Р(D) =0,0296. 37. Для работы технологической линии надо смонтировать установки А, В, С и D. Вероятность того, что установка А будет смонтирована к намеченному сроку равна - 0,9, В — 0,8, С — 0,7 и D - 0,6. Найти вероятность того, что линия не будет запущена в срок. Ответ: Р =0,6976.
38. Два города соединяют 5 линий связи, две из которых имеют надёжность 0,8, а три - 0,7. Найти вероятность того, что сообщение будет передано из одного города в другой. Ответ: Р(А) = 0,9989.
39. Надёжность элементов равна 0,8. Сколько таких элементов надо поставить (продублировать), чтобы надежность всей схемы была не менее 0,999? Ответ: n ³ 5.
40. В первом ящике находятся 1 белый, 2 красных и 3 синих шара, во втором - 2 белых, 6 - красных и 4 синих. Из каждого ящика случайным образом вынимают по одному шару. Найти вероятность того, что: А - оба шара красные; В - оба шара одинакового цвета. Ответ: Р(А) =0,1667, Р(В) = 0,3611.
41. Дано: Р(А) = 0,5, Р(В) = 0,7 и Р(А + В) = 0,9. Найти Р(А В), Р(В|А), Р(А В). Ответ: Р(А В) = 0,3, Р(В|А) = 0,6, Р(А В) = 0,2.
42. Имеются 10 карточек с цифрами: 0, 1,..., 9. Найти вероятность того, что при случайном отборе трёх карточек: А - последовательно появятся цифры 1, 2 и 5 (получится число 125); В - из появившихся цифр в итоге можно образовать число 125. Ответ: Р(А) = 0,001389, Р(В) = 0,008334.
43. Вода на станции очистки проходит последовательно через фильтры А, В и С. Вероятность того, что после первого фильтра вода будет полностью очищена от примесей равна 0,7, после второго - 0,6 и после третьего - 0,8. Найти вероятность того, что станция отпускает чистую воду. Ответ: Р(А) =0,976. 44. Прибор состоит из трёх узлов. Вероятность выхода из строя для первого узла равна 0,05, второго - 0,04 и третьего - 0,02. Найти вероятность того, что прибор выйдет из строя, если для этого достаточно выхода из строя хотя бы одного узла. Ответ: Р(А) = 0,1062.
45. Система электропривода станка защищена шестью одинаковыми плавкими предохранителями. Известно, что один из них перегорел. Найти вероятность того, что его удастся заменить на заведомо исправный: А - с первой попытки, В - со второй, будет сделано не более двух попыток. Ответ: Р(А) =0,1667, Р(В) =0,1667, Р(С) = 0,3333.
46. Предприятие выпускает массовым тиражом некоторые детали, причём вероятность появления брака в его продукции равна 0,05, и поставляет их другому предприятию. Выходной контроль на первом предприятии обнаруживает и не пропускает далее брак с вероятностью 0,9, а входной контроль на втором обнаруживает брак с вероятностью 0,95. Найти вероятность того, что: А - при выходном контроле будет обнаружена бракованная деталь; В - при входном контроле будет обнаружена бракованная деталь; С - деталь будет забракована; D - бракованная деталь будет пропущена. Ответ: Р(А) = 0,045, Р(В) = 0,00475, Р(С) = 0,04975, Р(D) = 0,00025.
47. Вероятность поражения цели при запуске одной зенитной ракеты равна 0,9. Сколько одновременно надо запустить таких ракет, чтобы цель была поражена с вероятностью не меньшей чем 0,999? Ответ: n ³ 3.
48. Система энергоснабжения предприятия трижды дублирована, причём надёжность первой линии равна 0,9, второй - 0,8 и третьей - 0,7. Найти: А - надёжность всей системы; В - вероятность выхода из строя двух линий; С - одной линии. Ответ: Р(А) = 0,994, Р(В) = 0,092, Р(С) = 0,398.
49. Одновременно бросаются две монеты. Пусть событие А есть появление герба на первой, В - появление герба на второй, С - появление на обеих монетах одновременно или герба или решки. Определить независимы ли события А, В и С попарно и в совокупности. (Указание: найти вероятности Р(А), Р(В), Р(С), Р(А В), Р(А С), Р(В С), Р(А В С) и проверить условие независимости). Ответ: Р(А) = Р(В) = Р(С) = 0,5, Р(А В) = Р(А С) = Р(В С) =0,25, Р(А В С) = 0,25 - попарно независимы; зависимы в совокупности. 50. (Гусарская дуэль). В барабане револьвера семь каналов, из них в пяти есть патроны, а два пустые. Барабан приводится во вращение и против ствола случайным образом оказывается один из каналов; после чего нажимается курок. Описанная процедура повторяется ещё раз. Найти вероятность того, что: А - в первый раз выстрел произойдёт, во второй не произойдёт; В - оба раза выстрелов не будет; С в первый раз выстрел не произойдёт, во второй произойдёт; D - будет два выстрела. Ответ: Р(А) = 0,3061, Р(В) = 0,08163, Р(С) = 0,2041, Р(D) = 0,4082.
51. В группе 10 хороших, 15 обычных и 5 плохих студентов. Из 50 подготовленных к зачёту задач хороший студент умеет решать 40, обычный - 30 и плохой - только 10. Найти вероятность того, что случайно выбранный студент сможет решить предложенную ему случайным образом задачу. Ответ: Р(А) = 0,6.
52. В дополнение к условию задачи 51 стало известно, что опрошенный студент задачу решил. Найти вероятность того, что это был: Н1 - хороший студент, Н2 - обычный и Н3 - плохой. Ответ: Р(Н1|А) = 0,4444, Р(Н2|А) =0,5, Р(Н3|А) = 0,0556.
53. Из 50 подготовленных к зачёту вопросов студент успел выучить только 30. Каким ему лучше идти сдавать - первым или вторым (если он идёт вторым, то на столе экзаменатора остается уже 49 вопросов). Ответ: Р(А1) = Р(А2) = 0,6 - безразлично каким.
54. Решить предыдущую задачу в более общей постановке: студент выучил не все вопросы, каким по порядку ему лучше сдавать: i-м или (i + 1) - м. Ответ: безразлично.
55. Имеются три одинаковые урны: в первой 5 белых и 5 чёрных шаров, во второй - 3 белых и 7 чёрных и в третьей - 2 белых и 8 чёрных. Из урны, выбранной наудачу, извлечён шар. Найти: А - вероятность того, что он белый; Н1 - вероятность того, что шар был взят из первой урны, если он оказался белым. Ответ: Р(А) = 0,3333, Р(Н1|А) = 0,5.
56. Изделия одного вида поставляют три фабрики: первая даёт 30% от всего количества, вторая - 25% и третья - всё остальное. Вероятность появления брака в продукции первой фабрики равна 0,01, второй - 0,02 и третьей - 0,03. Случайно отобранное и проверенное изделие оказалось бракованным. Найти вероятность того, что оно сделано на: первой, второй, третьей фабрике. Ответ: Р(Н1|А) = 0,1395, Р(Н2|А) = 0,2326, Р(Н3|А) =0,6279. 57. Два охотника сделали по одному выстрелу по кабану и убили его. Как по справедливости им надо разделить тушу, если оказалось, что попал только один и известно, что вероятность попадания в цель у первого стрелка равна 0,8, а у второго - 0,6. Ответ: в отношении Р(Н1|А) = 0,7273 к Р(Н2|А) = 0,2727.
58. Решить предыдущую задачу, если охотников было трое, в кабана попал только один и вероятности попадания в цель каждого из охотников соответственно равны 0,8, 0,7 и 0,6. Ответ: в отношении 0,5106: 0,2979: 0,1915.
59. Два населенных пункта А и В соединены дорогами, схема которых приведена. Найти вероятность того, что путешественник попадёт из В в А, если на развилке дорог он выбирает направление движения случайно. Ответ: Р(А) = 0,6111.
60. Три бригады ведут укладку бетонных блоков. Первая бригада выполнила 50% всего объёма работ, вторая - 30% и третья - всё остальное. Вероятность появления брака для первой бригады равна 0,05, второй - 0,06 и третьей - 0,1. Найти вероятность того, что: А - случайно выбранный блок установлен с допущением брака; Н3 - случайно выбранный и проверенный блок оказался установленным с допущением брака по вине третьей бригады. Ответ: Р(А) = 0,063, Р(Н3|А) = 0,3175.
61. Из имеющихся на складе 600 электроламп 200 изготовлены на первой фабрике, 250 - на второй и остальные на третьей. Вероятность того, что лампа стандартная для первой фабрики равна 0,95, для второй - 0,93 и третьей - 0,9. Случайно выбранная лампа оказалась нестандартной. Найти вероятность того, что она изготовлена на первой фабрике. Ответ: Р(Н1|А) = 0,2353.
62. Из имеющихся на складе 1000 мешков цемента 400 содержат качественный цемент с вероятностью 0,9, 350 - с вероятностью 0,8 и остальные - с вероятностью 0,6. Найти вероятность того, что случайно выбранный мешок содержит качественный цемент. Ответ: Р(А) = 0,79. 63. Из потребляемой кирпичным заводом глины 50% поступает с первого карьера, 30% - со второго и остальная с третьего. Вероятность получения качественной продукции из сырья, поставленного первым карьером равна 0,8, второго - 0,9 и третьего - 0,7. Найти процент качественной продукции, выпускаемой заводом. Ответ: 81% (Р(А) = 0,81).
64. В пирамиде из десяти винтовок только шесть пристреляны. Вероятность попадания в цель из пристрелянной винтовки у данного стрелка равна 0,8, а из непристрелянной - 0,5. Определить вероятность попадания в цель при одном выстреле, если стрелок выбирает винтовку случайным образом. Ответ: Р(А) = 0,68.
65. Из 30 студентов к экзамену отлично подготовились 5 (выучили все из 30 предложенных вопросов), 10 - хорошо (выучили 25), 10 - удовлетворительно (выучили 20) и 5 - плохо (знают только 10). Найти вероятность того, что случайно вызванный и опрошенный студент был: отлично подготовленным; плохо подготовленным студентом, если известно, что он правильно ответил на три произвольно заданных ему вопроса. Ответ: Р(Н1|А) = 0,3671, Р(Н4|А) = 0,01085.
66. В мастерской имеются четыре станка, каждый из которых может выйти из строя в течении смены с вероятностью 0,02. Найти вероятность того, что за одну смену из строя выйдут не более двух станков. Ответ: Р(0 £ m £ 2) = 0,999968.
67. Два равных по силе игрока играют в шахматы (ничьи не учитываются). Что вероятнее: первый выиграет три партии из шести, или четыре из восьми? Ответ: Р6(3) = 0,3125 ³ Р8(4) = 0,2734.
68. В мастерской установлены пять станков, каждый из которых требует наладки в течении рабочего дня с вероятностью 0,4. Найти вероятность того, что: ни один станок не потребует наладки; ровно два. Ответ: Р5(0) =0,07776, Р5(2) =0,3456.
69. Образец бетона выдерживает испытание на прочность с вероятностью 0,7. Испытывается 8 образцов. Найти вероятность того, что не менее 6 образцов выдержат испытания. Ответ: Р8(6 £ m £ 8) = 0,5518. 70. Вероятность того, что выпускаемые заводом телевизоры имеют дефекты, равна 0,02. Найти вероятность того, что из 10 проверенных телевизоров дефекты имеют не более чем два. Ответ: Р10(0 £ m £ 2) = 0,9991.
71. В круг вписан квадрат. В круг случайным образом брошено шесть точек (любое положение каждой точки в круге равновозможно). Найти вероятность того, что: хотя бы одна точка попадёт в квадрат; ровно одна. Ответ: р = 0,6367, Р6(1 £ m £ 6) = 0,9977, Р6(1) = 0,0242. 72. Студенту на зачёте предложено 10 вопросов, на каждый из которых надо дать ответ в виде “да” или “нет”. Найти вероятность того, что, отвечая наудачу (не зная), он сдаст зачёт, если для этого необходимо правильно ответить хотя бы на 7 вопросов. Ответ: Р10(7 £ m £ 10) = 0,1719.
73. В семье пять детей. Считая вероятность рождения мальчика и девочки равными 0,5, найти вероятность того, что в семье будет три девочки и два мальчика. Ответ: Р5(3) = 0,3125.
74. Вероятность того, что электролампа проработает не менее 1000 часов, равна 0,6. Найти вероятность того, что хотя бы одна из пяти ламп проработает этот срок. Ответ: Р5(1 £ m £ 5) = 1 - Р5(0) = 0,9898.
75. Вероятность того, что муфтовое соединение водопроводных труб при опрессовке не даст течи равна 0,9. Участок водопровода содержит восемь таких соединений. Найти вероятность того, что течь дадут: ровно два соединения; не более двух. Ответ: Р8(2) = 0,1488, Р8(0 £ m £ 2) = 0,9619.
76. В здании института установлено 600 светильников, каждый из которых может быть включён с вероятностью 0,6. Найти вероятность того, что: включено ровно 380 светильников; не более 380. Насколько светильников должна быть рассчитана подстанция, чтобы с вероятностью Р01 = 0,9 она могла бы обеспечить освещение института? Сколько ламп для светильников надо закупить, чтобы с вероятностью Р02 = 0,95 их хватило бы для замены во всех светильниках (600), если вероятность того, что каждая лампа хорошая, равна 0,75? Ответ: Р600(380) = 0,0083, Р600(0 £ m £ 380) = 0,9522, Р600(0 £ m £ k)³ Р01 Þ k ³ 376, Рn(600 £ m £ n) ³ Р02 Þ n ³ 828. 77. Вероятность повреждения железобетонных панелей при транспортировке равна 0,01. Найти вероятность того, что при перевозке 300 панелей будет повреждено: ровно две; не более трёх панелей. Ответ: Р300(2) = 0,224, Р300(0 £ m £ 3) = 0,6472.
78. Телефонный кабель состоит из 400 проводов. С какой вероятностью этим кабелем можно подсоединить 395 абонентов, если для каждого необходим один провод и вероятность того, что провод исправен, равна 0,3875. Ответ: Р400(0 £ m £ 5) = 0,616.
79. Доля высококачественных изделий в продукции фабрики равна 75%. Сколько таких изделий надо заказать, чтобы с вероятностью 0,9 среди них было бы не менее 700 высококачественных? Ответ: n ³ 956.
80. Вероятность появления бракованных деталей при их массовом производстве равна 0,002. Определить вероятность того, что в партии из 1500 деталей будет: ровно 3 бракованные детали; не более 3. Ответ: Р1500(3) = 0,224, Р1500(0 £ m £ 3) = 0,6472.
81. В механическом цехе работают 120 токарей. Вероятность того, что токарю потребуется инструмент определенного вида, равна 0,2. Сколько таких инструментов надо иметь в цехе, чтобы с вероятностью 0,95 удовлетворить потребность в них. Ответ: k ³ 32.
82. Вероятность того, что изготовленные на станке детали сразу пройдут ОТК, равна 0,8. Найти вероятность того, что из 6 деталей: ровно 4 пройдут ОТК; не менее 4. Ответ: Р6(4) = 0,2458, Р6(4 £ m £ 6) = 0,9011.
83. Согласно многолетним метеорологическим наблюдениям, в данной местности в среднем в сентябре бывает 12 дождливых (из 30) дней. Найти вероятность того, что в течение недели дождливыми окажутся: ровно три дня; не более трёх. Ответ: Р7(3) = 0,2903, Р7(0 £ m £ 3) = 0,7102.
84. Вероятность появления брака при обжиге керамических блоков в данной печи равна 0,05. Найти вероятность того, что среди пяти проверенных блоков: нет ни одного бракованного; ровно два бракованные. Ответ: Р5(0) = 0,7738, Р5(2) = 0,02143. 85. Вероятность появления брака при выпуске стеновых панелей на ЖБК равна 0,01. Найти вероятность того, что в партии из 200 панелей будет: ровно 4 бракованные; не более 4. Ответ: Р200(4)= 0,09022, Р200(0 £ m £ 4) =0,9473.
86. Вероятность попадания в цель при одном выстреле у данного стрелка равна 0,8. Найти вероятность выполнения им норматива, если для этого требуется попасть в цель не менее 70 раз при 100 выстрелах. Ответ: Р100(70 £ m £ 100) = 0,9938.
87. Вероятность заболевания гриппом во время эпидемии равна 0,3. Найти вероятность того, что из 2100 сотрудников предприятия заболеют: ровно 640; не более 650; от 600 до 650 сотрудников. Ответ: Р2100(640) = 0,01696, Р2100(0 £ m £ 650) = 0,8295, Р2100(600 £ m £ 650) = 0,7539.
88. 80% выпускаемых заводом высоконапорных железобетонных труб отпускаются потребителю первым сортом. Определить вероятность того, что в партии из 100 изделий будет: ровно 75 первосортных; не менее 75. Ответ: Р100(75) = 0,04565, Р100(75 £ m £ 100) = 0,8844.
89. Известно, что одним выстрелом стрелку почти невозможно попасть в самолёт. В то же время из практики войн известны случаи, когда при одновременной стрельбе целого подразделения самолеты сбивались. Принимая вероятность сбить самолёт при одном выстреле равной 0,001, найти вероятность поражения самолёта хотя бы один раз при стрельбе подразделением из 600 солдат. Ответ: Р600(1 £ m £ 600) = 1 - Р600(0) = 0,4512.
90. В опытах Резерфорда и Гейгера образец радиоактивного вещества испускал в среднем за 7,5 секунд 3,87 заряженных частиц. Найти вероятность того, что за одну секунду этот образец испустит хотя бы одну частицу. Ответ: Р(m ³ 1) =1 - Р(0) = 0,4031.
91. Средняя плотность частиц пыли в помещении, где производятся узлы электроники, равна 100 на 1м3 воздуха. Найти вероятность того, что во взятой пробе объёмом в 2 литра: не будут обнаружены частицы пыли; будет обнаружена хотя бы одна. Ответ: Р(0) = 0,8187, Р(m ³ 1) = 0,1813. 92. Минное заграждение представляет собой полосу шириной один километр, причём в среднем на 1 км2 приходится 100 мин. Найти вероятность того, что судно шириной 10 метров пройдёт беспрепятственно это заграждение, если его курс: А - перпендикулярен полосе; В - образует с ней угол 450. Ответ: Р(А) = 0,3679, Р(В) = 0,2431.
93. За одни сутки (24 часа) в среднем случается шесть аварий в системе водоснабжения. На сколько аварий в течении одной смены (8 часов) надо рассчитывать, чтобы с вероятностью не меньше 0,95 ремонтная служба могла с ними справиться? Ответ: k ³ 5.
94. Сколько доз определённого лекарства необходимо иметь в машине скорой помощи, чтобы его с вероятностью 0,98 хватило на всю смену (8 часов), если известно, что в среднем за сутки используется шесть доз такого лекарства? Ответ: k ³ 5.
95. Число заявок на ремонт, поступающих на диспетчерский пункт, представляет собой простейший (Пуассоновский) поток событий со средним числом две заявки в один час. Найти вероятность того, что за два часа поступит менее 4 заявок. Ответ: Р(m £ 3) = 0,4335.
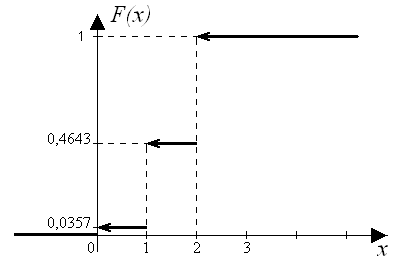
96. Найти вероятность того, что нейтрон пройдёт без столкновений с молекулами вещества (слоя радиационной защиты) расстояние L, рассматривая нейтроны и молекулы как шары радиусов r и R соответственно, а число молекул в единице объёма равным N. Как изменится эта величина для L1 = 2 L. Ответ: Р(L) = exp{-p L (r + R)2 N}, Р(L1) = [Р(L)]2. 97. В партии из 8 изделий 2 бракованных. Случайным образом отобраны два изделия. Случайная величина x - число хороших изделий, среди отобранных. Составить закон распределения, найти функцию распределения и построить её график, определить числовые характеристики. Ответ: М(x) = 1,5, D(x) = 0,3214
98. Вероятность попадания в цель у данного стрелка равна 0,6, стрельба ведётся до первого попадания, но не более трёх раз. Случайная величина x - число сделанных выстрелов. Составить закон распределения, найти функцию распределения и построить её график, определить числовые характеристики. Ответ: М(x) = 1,56, D(x) = 0,5664
99. В урне 5 белых и 15 чёрных шаров. Случайным образом вынули три шара. Случайная величина x - число вынутых белых шаров. Составить закон распределения, найти функцию распределения и построить её график, определить числовые характеристики. Ответ М(x) = 0,75, D(x) = 0,5035
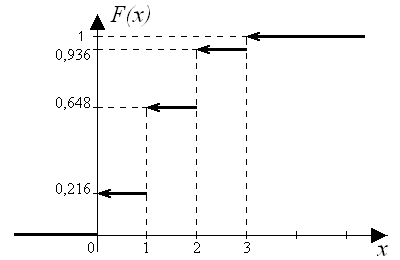
100. Случайная величина x - число попаданий в корзину мячом. Составить закон распределения, найти функцию распределения и построить её график, определить числовые характеристики, если баскетболист делает три броска и вероятность попадания в корзину при одном броске у него равна 0,4. Ответ: М(x) = 1,2, D(x) = 0,72
101. В книжной лотерее продано 100 билетов стоимостью один рубль каждый. Разыгрывается четыре книги стоимостью 40, 16, 8 и 4 рубля (на один билет не более одной книги). Найти математическое ожидание чистого выигрыша для человека, купившего: А - один билет, В - два билета (стоимость книг минус стоимость билетов). Ответ: М(x) = -0,32 руб., М(x) = -0,64 руб.
102. Стрелок делает три выстрела по мишени с вероятностью попадания в цель при одном выстреле равной 0,6. Составить закон распределения случайной величины x - числа попаданий, найти функцию распределения и числовые характеристики. Ответ: М(x) = 1,8, D(x) = 0,72.
103. При установке бракованного узла в прибор он при включении полностью выходит из строя. Определить, будет ли экономически целесообразно проводить сплошной контроль указанных узлов при массовом производстве, если стоимость контроля каждого узла после изготовления равна 1 руб., а стоимость всего прибора - 200 руб. и вероятность изготовления бракованного узла равна: а - 0,01; б - 0,001 (вычислить и сравнить математические ожидания убытка в этих случаях с затратами на сплошной контроль узлов). Ответ: а) - целесообразно М(x) = 2 руб., б) - нецелесообразно М(x) = 0,2 руб.
104 Согласно статистическим данным вероятность того, что двадцатипятилетний человек проживёт ещё один год, равна 0,992. Страховая компания предлагает такому клиенту застраховать свою жизнь на год на любую сумму при страховом взносе 1% от этой суммы. Будет ли это выгодно для страховой компании? Ответ: да, так как математическое ожидание случайной величины x - дохода компании в этом случае М(x) = 0,002 А > 0, где А - сумма страхового полиса.
105. Задана плотность вероятности непрерывной случайной величины x. Найти коэффициент А, функцию распределения и числовые характеристики. Ответ: А = 0,5, М(x) = 1,5833, D(x) = 0,07639,
106. Задана плотность вероятности непрерывной случайной величины x. Найти коэффициент А, числовые характеристики и вероятность того, что случайная величина примет значения в интервале Ответ: А = 0,5, М(x) = 1,5708, D(x) = 1,4674, Р(0 £ x £
107. Задана плотность вероятности непрерывной случайной величины x (распределение Лапласа) Ответ: А = 0,5, М(x) = 0, D(x) = 1, Р(0 £ x £ 1) = 0,3161.
108. Задана плотность вероятности непрерывной случайной величины x (отражённое нормальное распределение). Найти коэффициент А, функцию распределения и числовые характеристики. Ответ: А = М(x) =
109. Задана функция распределения непрерывной случайной величины x. Найти коэффициенты А и В, плотность вероятности и числовые характеристики. Ответ: А = 0,5, В = 1, М(x) = 0, D(x) =
110. Задана функция распределения непрерывной случайной величины x. Определить коэффициенты А, В, С, D. Найти плотность вероятности, числовые характеристики и вероятность того, что случайная величина примет значение в интервале [0,5, 3]. Построить графики функции распределения и плотности вероятности. Ответ: А = 0, В = 0,5, С = М(x) = 0, D(x) = 0,5 Р(0,5 £ x £ 3) = 0,3333.
111. Задан график плотности вероятности непрерывной случайной величины x. Найти коэффициент А, аналитические выражения для и, числовые характеристики и вероятность попадания случайной величины x в интервал [1, 3]. Построить график функции распределения. Ответ: А = 0,5, М(x) = 2, D(x) = 0,6667, Р(1 £ x £ 3) = 0,75.
112. Известна функция распределения непрерывной случайной величины x: F(x) = A + B arctg x (распределение Коши). Найти коэффициенты А и В, плотность вероятности, математическое ожидание и вероятность попадания случайной величины в интервал [0, 1]. Построить графики f(x) и F(x). Ответ: А = 0, В = Р(0 £ x £ 1) = 0,25
113. Точка брошена в круг радиуса R так, что любое её положение в круге равновозможно. Найти функцию распределения, плотность вероятности и числовые характеристики случайной величины x - расстояния от точки до центра круга. Ответ: М(x) =
114. Рассматривая прочность качественной стальной проволоки, идущей на изготовление тросов, как нормально распределённую случайную величину x с М(x) = 300 кГ/мм2 и s(x) = 20 кГ/мм2 , найти вероятность того, что: а) 280 £ x £ 340, б) x ³ 270. Ответ: Р(280 £ x £ 340) =0,8185, Р(270 £ x < ¥) = 0,9332.
115. Вес мешка цемента - случайная величина, распределённая по нормальному закону с математическим ожиданием 50кг и среднеквадратическим отклонением 0,5кг. Найти вероятность того, что вес одного мешка будет не меньше 49 кг; вес каждого из двух мешков будет не меньше 49кг. Ответ: Р(x ³ 49) = 0,9772, (Р(x ³ 49))2 = 0,9540.
116. Удельный вес тяжёлого бетона можно рассматривать как случайную величину, распределённую по нормальному закону с математическим ожиданием 2200 кГ/м3 и среднеквадратическим отклонением 200 кГ/м3. Найти вероятность того, что удельный вес бетона не превзойдёт 2500 кГ/м3. Ответ: Р(x £ 2500) = 0,9332. 117. Некоторая игра заключается в бросании трёх игральных костей и подсчёте числа выпавших очков - случайной величины x. Выигрыш пропорционален квадрату числа выпавших шестёрок с коэффициентом пропорциональности К. Найти математическое ожидание и дисперсию случайной величины h - величины выигрыша (h = К x2). Ответ: М(h) = 0,6667 К, D(h) = 1,3889 К2.
118. Сторона квадратного участка измерена приближенно (в метрах). Рассматривая длину стороны как случайную величину, равномерно распределённую в интервале [100, 110], найти числовые характеристики S - площади участка. Ответ: М(S) = 11033 м2, D(S) = 367556 м4.
119. Характерный размер частиц гравия (в сантиметрах) после сортировки по фракциям можно рассматривать как случайную величину x, равномерно распределённую в интервале [5, 7]. Найти числовые характеристики случайной величины h - веса частиц гравия, считая, что он пропорционален кубу характерного размера с коэффициен
|

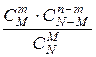 .
. 25. В круг случайным образом брошена точка так, что любое её положение в круге равновозможно. Найти вероятность того, что она окажется внутри: А - вписанного в круг квадрата; В - вписанного в круг равностороннего треугольника.
25. В круг случайным образом брошена точка так, что любое её положение в круге равновозможно. Найти вероятность того, что она окажется внутри: А - вписанного в круг квадрата; В - вписанного в круг равностороннего треугольника. ;
; 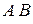 ;
; 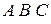 ;
;  ;
;  ;
; 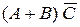 ;
; 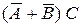 .
.




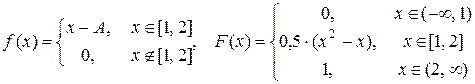 .
.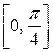 .
.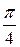 ) =0,1464,
) =0,1464, .
.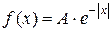 . Найти коэффициент А, функцию распределения, числовые характеристики и вероятность того, что x примет значения в интервале [0, 1].
. Найти коэффициент А, функцию распределения, числовые характеристики и вероятность того, что x примет значения в интервале [0, 1].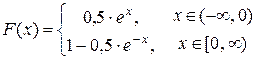 .
. = 0,7979, D(x) = 1 -
= 0,7979, D(x) = 1 -  = 0,3634,
= 0,3634,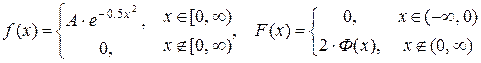 .
. = 1,4674,
= 1,4674, .
.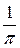 , D =1,
, D =1,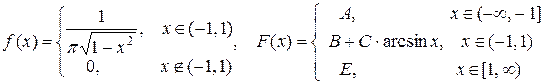 .
.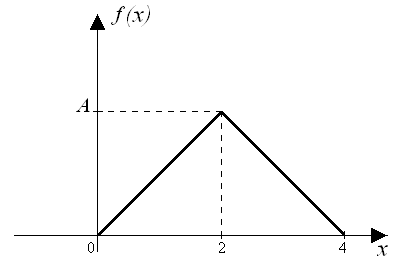
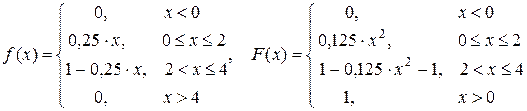 .
. , D(x) =
, D(x) = 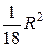 ,
, .
.


